Bohr atom revisited

1. Potential energy of the electron

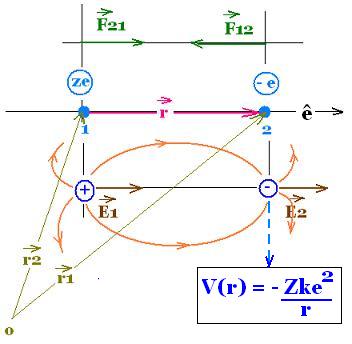
The coulomb force exerted by 1 (Z potons of charge +Ze) on 2 
(electron of charge -e) is F12. Its expression is the following 
Coulomb force:
F21 = F12 = (1/4πε0) q1 q2/ r2 ê

F12 is the force exerted by 1 on 2, that is rhe force exerted 
by the nucleus(Z protons) on the electron.

With 1/4πε0 = k = 8.987 x 10 9 N.m2/C2, q1 = +Ze and q2 = -e,
we obtain:
F12 = - Ze2k/r2ê 
(r1 - r2 = r = |r| ê, ê is the unit vector with the 
line from the charge 1 to the charge 2).

The related electric field is E2 = Ee = F12/q2 = F12/(-e)
= + Zek/r2ê 

Since F12 = - ∇V2 = - dV2(r)/dr, where V2 (r) is the 
related electric potential, 
we can write:

V2(r) = - ∫ F12 = - ∫ - Ze2k/r2ê  dr =
+ Ze2k ∫ 1/r2 dr  = - Ze2k/r + cst.

We choose at infinity (∞) the potential energy is 
zero, therefore cst = 0, and 

V2(r) = - Ze2k/r

On the electron in atom:

Coulomb force: F12 = Fc =  - Zke2/r2  ê 
Electric field: E2 = + Zke/r2  ê 


Potential energy: V(r) = - Zke2/r


k = 1/4πε0 = 8.987 x 10 9 N.m2/C2

2. Bohr's atom

2.1. Bohr's radius atom

The Coulomb force provides the centripetal 
force required for the electron to keep it moving in 
the circular path. 

The electrostatic force and the centripetal force are aligned, 
of opposite direction and equal in magnitude. Therefore:

F12 = mv2/r 
Ze2k/r2 = mv2/r

Thus:

Ze2k/r = mv2


The quantification of the linear momentum of the 
orbiting electron is written as:

L = mvr = n ℏ

Combinig the two ferm relations yields:
(Ze2k/r2)(r) = mv2 = m n2 ℏ2/ m2 r2 
Ze2k/r =  n2 ℏ2/ m r2 
Therefore:
Ze2k  = n2 ℏ2/ m r

r = (ℏ2/m e2 k) n2 /Z 

ℏ = 1.05 x 10-34 J s 
k = 8.987 x 10 9 N.m2/C2
e = 1.60 x 10-19 C
m = 9.11  x 10-31kg


The bohr radius a0 = 
ℏ2/me2 k = 
(1.05 x 10-34)2/ 9.11  x 10-31 (1.60 x 10-19)2 8.987 x 10 9 =  
0.0053 x 10-68 + 31 + 38 -9  = 0.53 x 10-10 m = 0.53 Angstrom.

Then:
r = a0 n2 /Z

For the hydrogen atom, n = 1, and Z = 1, then: 
r = a0 = 0.5 Angstrom.

2.2. Bohr's energies atom

The total energy is E = KE + PE 
KE = (1/2)mv2 
PE = - Ze2k/r

From the equality F(Coulomb) =  F(Centripetal)
Ze2k/r2 = mv2/r, we have:
- PE = 2 KE , so:
E = KE - 2KE = - KE = + EP/2 = - Ze2k/2r = 

Using the expression of r: 
r = (ℏ2/m e2 k) n2 /Z
We find:
E = - Ze2k . m e2 k/2ℏ2 Z /n2 =  - me4k2/2ℏ2 (Z2/n2) 

E =  - me4k2/2ℏ2 (Z2/n2) 


ℏ = 1.05 x 10-34 J s 
k = k = 8.987 x 10 9 N.m2/C2
e = 1.60 x 10-19 C
m = 9.11  x 10-31 kg

me4k2/2ℏ2 = 9.11 . (1.60)4 . 8.9872/2. (1.05)2
= 2183.44 x 10-31 -76 + 18 + 68 Joules = 
2183.44 x 10-21 Joules  = 1364.65 x 10-21+19eV =  
13.6 eV

Therefore:

E = - 13.6 (Z2/n2) eV

2.3. Speed of the electron in the atom

The energy of the electron is entirely kinetic. So, 

 E = - KE = - (1/2) mv2 = - 13.6 Z2/n2

Let Eo = 13.6 eV. Therefore:

v2 = (2 x Eo/m) Z2/n2

v = (2Eo/m)1/2 Z/n

Eo = 13.6 eV = 13.6 x 1,6 x 10-19 J
v = (2 x 13.6 x 1.6 x 10-19/9.11  x 10-31)1/2 Z/n

v (electron) = 2.2 x 106  Z/n  (m/s)