Length Contraction

1. Length Contraction

Now, let's consider the mirror attached in o'x' axis as
chown in figure 3. For the the moving observer in its
moving frame x'o'x', if  a flash is sent from o', it will reach 
Mirror and reflect back with the time t' = 2L'/c.  (4)





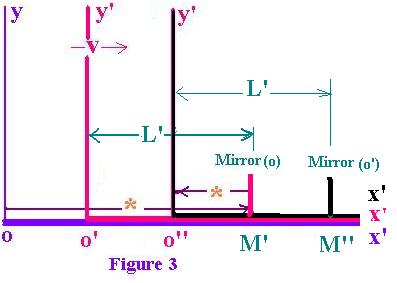
For the stationary observer, the situation is differente:
When the flash leaves from o' and reached Mirror, at
this precise time, the observer o' has moved to o' .
(supposed o=o' at first).


We have oo' = vt1 and oMirror = ct1
t1 is the time taken by the flash to go
from o to Mirror at the position M'.
We can write:
ct1 = oo' + L	
( L is the distance between o' and Mirror for the observer in
the stationary xoy frame)
Thus:
ct 1= vt1 + L    (5)

The flash reflects back and reaches the observer o' at
the position o'' while the observer o' has moved 
from o' to o'' (The Mirror from M' to M'')
the related time to reflect back to the observer to o'
is t2.
We can write ct2 = L - v t2    (6)

The total time taken by the flash for its round trip is
t= t1 + t2
from (5) and from (6):
t = (L/ (c-v)  +  L/(c+v) = 2Lc/ c2  - v2 

t =  g2. 2L/c    (7)

Solving for L', we have:
from (4) and from (3):
L' = ct'/2 = (c/2)(t/g)
And from (7)

L' = g L  (8)					





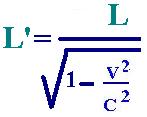
The factor g is greater than 1. Then L is smaller that L'.
For the observer at rest, the length is shorter than the length
in the moving frame is.

2. Example:

In a moving reference frame, Frank , at rest, 
measures a the density of a cube and find d = m/V 
m/L'3 = 2.0 kg/m3

This Frank-frame moves at the speed v = 0.92 c with 
respect to the fixed Carmen-frame.

Carmen wants to know the density of the cube 
in her frame.

Just the longitunal side is contracted foe 
her: L' → L = L'/γ
γ = 1/( 1 - v2/c2)1/2. Therefore:
d' = m/(L'/γ)L'L' = d' = γ m/(L'L'L') = γd

γ = 1/( 1 - (0.92)2/c2)1/2 = 2.55

Therefore:
d' = 2.55 x 2.0 = 5.10 kg/m3.