Contents
Special Relativity
© The scientific sentence. 2010
|
Time Dilation
In this lecture, we assume that the speed of light
is independent of the speed of the source.
Time Dilation
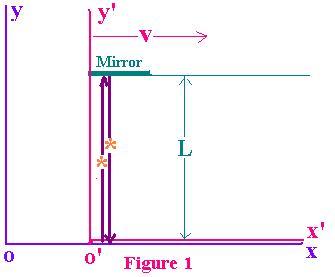
Let's consider the figure 1. The reference frame xoy is at rest. The
reference frame x'o'y' is moving at the speed v in the direction o
towards o'. The frame x'oy' carries a mirror at the distance L from the
observer o' . If the observer in the frame x'oy' send a flash in the
direction o'y', this flash will reach
the mirror and then reflect back to arrive to this observer
in the point o'. The time for this travel is :
t' = L/c + L/c = 2L/c (1)
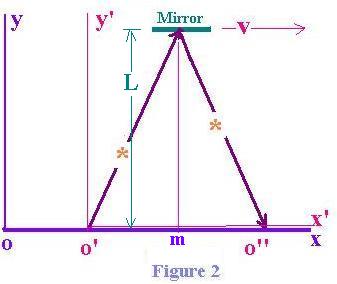
For the observer in the farme at rest xoy, the situation is differente. It's
related to the figure 2. When the flash returned back to the observer o',
the frame x'o'y' (observer o' along with the mirror) were moved with the
speed v. The observer o' moved from o to o'. At this precise position o',
this observer o' receives the emitted flash sent the time t before.
The flash has travelled ct/2 ( from o to Mirror) + ct/2
(from Mirror to the o') = ct.
We can write:
(ct/2)2 = (o'm)2 + L2 (2)
o'm = vt/2,
L = ct'/2, from the equation (1)
Thus:
(ct/2)2 = (vt/2)2 + (ct'/2)2
Resolving for t', we get:
(ct'/2)2 = (ct/2)2 - (vt/2)2
t' 2 = (2/c) 2 (t/2)2 ( c2 -(v)2)
t' 2 = (t)2 ( 1 - (v)2/(c)2)
t' 2 = (t)2 ( 1/ γ 2)
t' = t/γ
or
t = γt' (3)
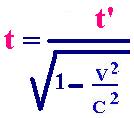
The factor g is greater than 1. Then t is greater that t'.
For the observer at rest, the time is longer than the time
in the moving frame is.
|
|