Contents
Special Relativity
© The scientific sentence. 2010
|
Physics: Lagrange equation
1. Euler Lagrange equation
When a particle of mass m moves along a displacement x(t), with a speed v(t)
from an initial time ti to a final time tf, we can
express this motion by a function L(x(t),x'(t)). This function has dimension
of energy.
We want to find an equation for this function using the least action
principle.
We will use the notations: x(t) = p(t) and
v(t) = q(t), so q(t) = dp(t)/dt.
The action of the particle is by definition :
S = ∫ dt L(p(t), q(t))
from ti to tf
S = ∫dt L(p(t), q(t))
from ti to tf
The variation δS can be written as δS =
δ ∫ dt L(p(t),q(t)) = ∫ dt δL(p(t),q(t))
from ti to tf
The action is minimum if the variation δS is
zero.
δS = 0
δS = 0
That is
δ ∫ dt L(p(t),q(t)) = ∫ dt δL(p(t),q(t)) = 0
from ti to tf
The variation δL(p(t),q(t)) can be written as a total differential:
δL(p(t),q(t)) = [∂L/∂p]δp + [∂L/∂q]δq
∫ dt[∂L/∂p]δp + ∫ dt[[∂L/∂q]δq = 0
With δq = d(δp)/dt, we have:
∫ dt[∂L/∂p]δp + ∫ dt[[∂L/∂q] d(δp)/dt = 0
The function L(p(t),q(t)) does not depend on the variable time t, so
∫ dt[∂L/∂p]δp + ∫ dt [∂L/∂q] d(δp)/dt = 0
The second term of this equation can be integrated by parts:
Let:
u = ∂L/∂q
du d(∂L/∂q)/dt . dt
v = δp
dv = d(δp)/dt . dt
Therefore
∫ dt [∂L/∂q] d(δp)/dt = ∫ u dv = uv - ∫ vdu =
(∂L/∂q)δp - ∫ δp . d(∂L/∂q)/dt . dt
from ti to tf
(∂L/∂q)δp = 0
from ti to tf
It remains:
∫ dt[∂L/∂p]δp - ∫ δp . d(∂L/∂q)/dt . dt = 0
from ti to tf
=
∫ dt{(∂L/∂p) - d(∂L/∂q)/dt} δp dt = 0
from ti to tf
(∂L/∂p) - d(∂L/∂q)/dt = 0
That the Euler- Lagrange equation
∂L/∂p = d(∂L/∂q)/dt
2. Examples: Energy function
2.1. Moving particle in a field
A particle of mass m, moving along a displacement
z,
with a potential energy V(z), and a velocity v, has
the following energy function:
The Lagrangian energy function is set to be
equal to the difference between kinetic energy
and potential energy.
The kinetic energy is: (1/2)mv²
The potetial energy is: V(z)
L(z,v) = (1/2)mv² - V(z)
∂L/∂p = ∂L/∂z = - ∂V(z)/∂z
d(∂L/∂q)/dt = d(∂L/∂v)/dt = d(mv)/dt = m a
a is the acceleration of the particle. If the force acting on the
particle is conservative, then - ∂V(z)/∂z = F , and
we find Newton second law F = ma.
2.2. Simple pendulum
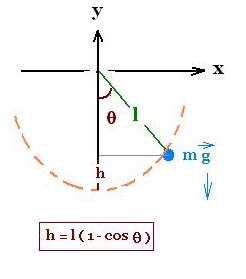
Consider a simple pendulum composed of an object of mass m
and a massless string of constant length "l" in a gravitational
field with acceleration g.
The motion of the pendulum is two-dimensional. The position of
the object is:
x = l sin θ
y = l cos θ
The related velocity is:
x' = dx/dt = l cos θ dθ/dt
y' = dy/dt = - l sin θ dθ/dt
so
v² = x'² + y'² = l²(dθ/dt)²
The kinetic energy is
KE = (1/2) m v² = (1/2) m l²(dθ/dt)²
The zero-potential energy is chosen at θ = 0, so
the potential energy at the position θ is:
PE = m g h = mgl(1 - cos θ)
The Lagrangian is:
L (θ, θ') = KE - PE = (1/2) m l²(dθ/dt)² - mgl(1 - cos θ)
With
θ' = θ/dt
We have:
∂L/∂θ = - mglsin θ
and
∂L/∂θ' = m l² (dθ/dt)
d(∂L/∂θ')/dt = m l² (d² θ/dt²)
The Euler-Lagrange equation is:
- mglsin θ = m l² (d² θ/dt²)
That is:
d² θ/dt² + (g/l)sin θ = 0
d²θ/dt² + (g/l)sin θ = 0
For small θ, we have:
d² θ/dt² + (g/l)θ = 0
d²θ/dt² + (g/l)θ = 0
This is the equation of the motion of a simple pendulum.
|
|