Contents
Special Relativity
© The scientific sentence. 2010
| Momentum in relativity
In this paragraph, we will find the expression of the relativistic
momentum; using an elastic collision.
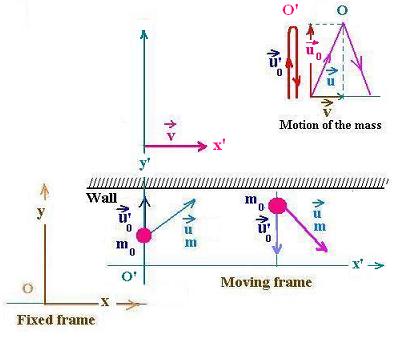
Let's consider that the inertial frame O'x'y' moves at constant
velocity v with respect to the frame Oxy.
In the moving frame O'x'y',
an object of mass m0 goes upwards with velocity u'0, hits the wall
and returns backwards with velocity - u'0.
Before collision:
- The linear momentum of the object is m0u'0
- The linear momentum of the wall is 0
After collision:
- The linear momentum of the object is - m0u'0
- The linear momentum of the wall is 0
The change in the momentum is:
ΔP'0 = (+ m0u'0) - ( - m0u'0) = 2m0u'0
ΔP0 = 2m0u'0
In the fixed frame Oxy, for the moving frame,
the object has the mass m, goes upwards with velocity: u = v + u0,
hits the wall and returns backwards with velocity: u = v - u0.
u0 is the velocity measured from the fixed frame
for the moving frame where the velocity of the object is u'0.
The y-component Lorentz velocity transformation gives:
u0 = u'0/γ
γ = 1/[1 - v2/c2]1/2
(u0 over the x axis is null in the moving frame)
Before collision:
- The linear momentum of the object is: m(u0 + v)
- The linear momentum of the wall is 0
After collision:
- The linear momentum of the object is: m (v - u0)
- The linear momentum of the wall is 0
The change in the momentum measured in the frame at rest Oxy is:
ΔPx = ( + mv) - ( + mv) = 0 over x axis.
and Py = (+ mu0) - ( - mu0) = 2mu0 over y axis.
ΔPx = 2mu0 = 2mu'0/γ
The change in the momentum is the same in the
two inertial frames.
Therefore:
ΔP'0 = ΔPx
That is:
2m0u'0 = 2mu'0/γ
Hence:
m0 = m/γ
Therefore:
m = γ m0
m = m0/[1 - v2/c2]1/2
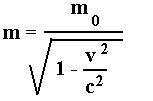
If an object of mass m0 at rest, moves at velocity v,
its relativistic momentum is P = mv = γm0v.
|
|