Contents
Special Relativity
© The scientific sentence. 2010
| Simultaneity
1. Definition
In galilean relativity, the time is considered absolute,
that is the same for all the observers in different frames
.
If two events occured at the same time, that is simultaneously,
in one reference frame, they are also simultaneous in all
reference frames.
This absolute simultaneity is not valid.
According to Lorentz transformastionx , we have:
x'= γ(x - vt ),
t' = γ (t- vx/c2),
If, in a frame, two simultaneous events (x1,t1) and (x2,t2)
occur , we have t1 = t2, that is Δt = t2 - t1
In another frame O' moving at a speed v with respect to the
first frame O, we have:
Δt' = t'2 - t'1 = γ (t2- vx2/c2) - γ (t1- vx1/c2) =
γ [(t2 - t1) - v(x2 - x1)/c2)] = - γ vΔ/c2)]
Since Δt' is not zero, these two events are not
simultaneous in the new frame O'. Two observers in different
frames do never agree on events being simultaneous.
2. Example Vaulter's pole through a barn
 v = 0.888 c
β = 0.888
(1 - β2)1/2 =
(1 - (0.888)2)1/2 = 0.46
γ = 1/(1 - β2)1/2 = 2.17
To make things simple let's set γ = 2
v = 0.888 c
β = 0.888
(1 - β2)1/2 =
(1 - (0.888)2)1/2 = 0.46
γ = 1/(1 - β2)1/2 = 2.17
To make things simple let's set γ = 2
2.1. Points of view of observers
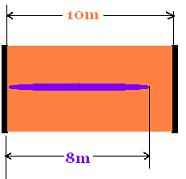
Barn's frame:
The barn's length is 10 m
The pole is moving at v = 0.888c toward me (the barn),
its length is contracted by γ, that is 16m/γ =
16/2 = 8 m.
Therefore the pole's length (8 m) is enough to get in
the barn and then close the two doors of the barn.
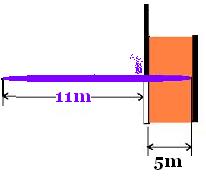
 Pole's frame:
The pole's length is 16 m
The barn is moving at v = - 0.888c toward me (the pole),
its length is contracted by γ, that is 10m/γ
= 10/2 = 5 m.
Therefore the barn's length (5 m) is insufficient
to contain the pole (16 m). If the two doors close
just as the front tip of the pole reaches the back
door, the pole will break off the last
16 - 5 = 11 m of the pole:
Pole's frame:
The pole's length is 16 m
The barn is moving at v = - 0.888c toward me (the pole),
its length is contracted by γ, that is 10m/γ
= 10/2 = 5 m.
Therefore the barn's length (5 m) is insufficient
to contain the pole (16 m). If the two doors close
just as the front tip of the pole reaches the back
door, the pole will break off the last
16 - 5 = 11 m of the pole:
2.2 Simultaneity
Let's set the following events:
For the barn:
We close the two doors at t = 0, therefore:
Event1 (closing the left door) = (x1 = 0 , t1 = 0)
Event2 (closing the right door) = (x2 = 10m , t2 = 0)
These two events are simultaneous in the frame
of the barn.
For the pole:
Right now at t'1 = 0 and x'1 = 0, the right door is
already closed. This right door was closed at t'2 = - 0.058µs
(already 0.058µs ), the right door closed 0.058
before the left closes. This time is taken by the barn
to move toward the pole, then the related displacement
is 0.058µs x 0.888c = 15m.
Event'2 (closing the right door) = (x'2 = 20, t'2 = - 0.058 µs )
Event'1 (closing the left door) = (x'1 = 0, t'1 = 0)
The left door closes at t'1 = 0 and the right dooe
was already closed 0.058 µs before. These two
events Event'1 and Event'2 are not simultaneous.
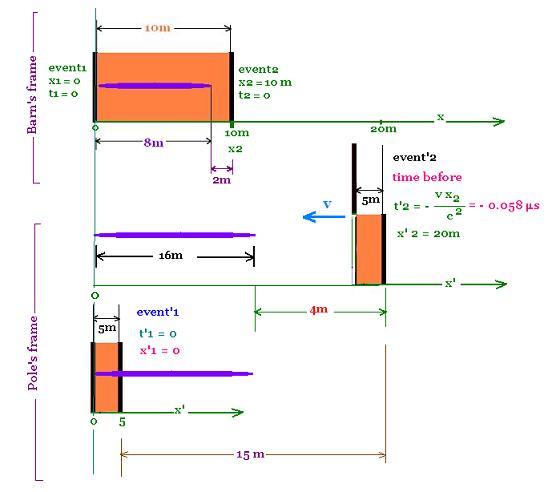 Another event:
Let's consider the event3 at x'2 = 16m:
The right door of the barn closed at x2 = 20 m and at
the time t = - 0.058 µs. By moving left toward
the pole, the right door reached the front tip of the
pole at x'2 = 16 m after traveling 20 - 16 = 4 m, that
corresponds to the time = - 0.058 µs + 4 m/0.888c µs =
- 0.058 µs + 0.015 µs = - 0.0423 µs.
We can write for the event 3 = event'2 at x' = 16m:
Event3 = (x'2, t'2) = (16 m, -0.043µs)
Next, verify the value of the time t'2 by using Lorentz's
transformations:
x'3 = γ(x2 - vt2)
x2 and t2 are the space time coordinates of the tip of the
pole in the barn frame. That is x2 = 10 - 8 = 2 and t2 = 2/0.888c
= 0.0077 µs
x'3= γ(10 - 0.888c x 0.0075 µs ) = 16 m,
t'2 = γ (t2 - vx2/c2) = 2(0.007 - 0.888 x 10/c)
= - 0.043
Therefore, the results agree.
Another event:
Let's consider the event3 at x'2 = 16m:
The right door of the barn closed at x2 = 20 m and at
the time t = - 0.058 µs. By moving left toward
the pole, the right door reached the front tip of the
pole at x'2 = 16 m after traveling 20 - 16 = 4 m, that
corresponds to the time = - 0.058 µs + 4 m/0.888c µs =
- 0.058 µs + 0.015 µs = - 0.0423 µs.
We can write for the event 3 = event'2 at x' = 16m:
Event3 = (x'2, t'2) = (16 m, -0.043µs)
Next, verify the value of the time t'2 by using Lorentz's
transformations:
x'3 = γ(x2 - vt2)
x2 and t2 are the space time coordinates of the tip of the
pole in the barn frame. That is x2 = 10 - 8 = 2 and t2 = 2/0.888c
= 0.0077 µs
x'3= γ(10 - 0.888c x 0.0075 µs ) = 16 m,
t'2 = γ (t2 - vx2/c2) = 2(0.007 - 0.888 x 10/c)
= - 0.043
Therefore, the results agree.
|
|