Contents
Special Relativity
© The scientific sentence. 2010
| Lorentz Transformations
1. Lorentz Transformations
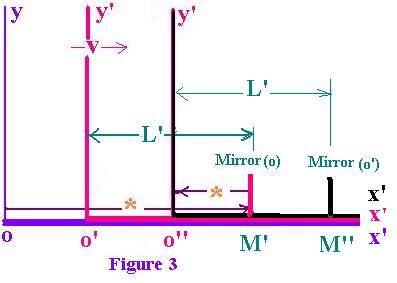 Now, for the observer in its farme xo'y', o'M' = o"M'".
Let's write it equal to x'.
At t'0, the flash leaves o' and at t' it
reaches the point x'.
Thus, for the moving observer,
c( t' - t'0) = L' = x' (9)
Now, for the observer in its farme xo'y', o'M' = o"M'".
Let's write it equal to x'.
At t'0, the flash leaves o' and at t' it
reaches the point x'.
Thus, for the moving observer,
c( t' - t'0) = L' = x' (9)
For the observer at rest, we have:
oM' = x
and c(t - t0) = oo' + L
= v. (t - t0) + L
Then :
(t - t0) = L/(c-v) (10)
Let's consider :
At x = 0, t0= 0.
Then ct = x ,
that is:
x = vt +L (11)
Solving for L :
L = x-vt (12)
Using the relation (8) : L' = gL
(12) becomes:
L' = g(x-vt)
or x' = g(x-vt) (13)
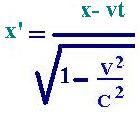
(9) gives:
t' = x'/c + t'0
Using (13) :
t' = g(x-vt)/c + t'0
Using the dilatation formula ( relation(3)):
t 0= gt'0
We have then:
t' = g(x-vt)/c + t0/g
Using the contraction formula ( relation(8)):
t 0 = t - L/(c-v) = t - (x-vt)/(c-v)
Thus:
t' = g(x-vt)/c + t/g - (x-vt)/(c-v)/g = g(x-vt)/c +
(ct -x)/(c-v)g
= g( (x-vt)/c) + (ct-x)/(c-v).g2 )
= g( (x-vt)/c) +(ct-x)(c+v)/c2)
= g/c2(c2t -xv)
= g(t -xv/c2)
t' = = g(t -xv/c2) (14)
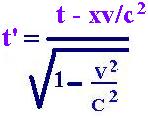
Since there is no change with y ans z
axis, we have y = y' and z= z'
When a reference frame (x'y'z't') moves at a speed v relating
to the reference frame at rest (xyzt), the relationships between
these coordinates are known as the Lorentz transformations
and grouped as fellow:
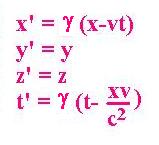
Remark:
In the case of very low velocities, g is near to 1, furthermore,
the Lorentz transformations become Galileo transformations.
2. Lorentz Inverse Transformations
The transformations above are set by the stationary observer
for whom the farme x'o'y' is moving at the speed +v.
The inverse transormation are obtained when the observers change the
roles. That is, for the observer in x'o'y', we have the same transformations
related to the frame xoy moving at the speed -v:
( Changing prime in no prime and vis versa , - in +)
We have:
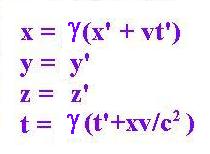
3. Lorentz Velocities Transformations
We are interested now to set the transformations of the components
of a certain vector velocity V ( Vx, Vy, Vz) related to V' ( V'x, V'y, V'z) .
From the relations above, we have the following differentiations:
dx = g(dx' + vdt'`)
dt = g(dt' + dx'v/c2)
dx/dt = Vx, the component of the velocity over ox.
Vx = (V'x + v)/(1 + V'x.v/c2)
Where V'x = dx'/dt' is the component of the velocity V' over o'x',
and v is the relative velocity of the frame
Vy = dy/dt = dy'/dt' = dy'/g(dt' + dx'v/c2)
= V'y/g(1 + dx'v/c2/dt')
= V'y/g(1 + V'x v/c2)
Vz = V'z/g(1 + V'x v/c2)
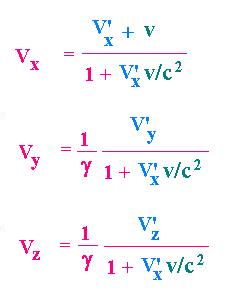
Remark that, it the moving observer in (x',y',z') referencial
frame meseares the velocity of light in this frame and finds
V'x = c , the first relation gives also Vx =c.
The conclusion is the speed of light is the same in these two
referential frames.
|
|