Analyse
ses théorèmes
L'Analyse
Les fonctions
Continuité
Dérivabilité
Différentiabilité
Théorème des valeurs extrêmes
Théorème des valeurs intermédiaires
Théorème de la moyenne
Théorème de Rolle
Théorème de la moyenne généralisé
Théorème de Fermat
Théorème de L'Hospital
Encadrement d’une valeur
Méthode de balayage
© The scientific sentence. 2010
|
Calcul différentiel et integral
Extrema d'une fonction
Extrema d'une fonction
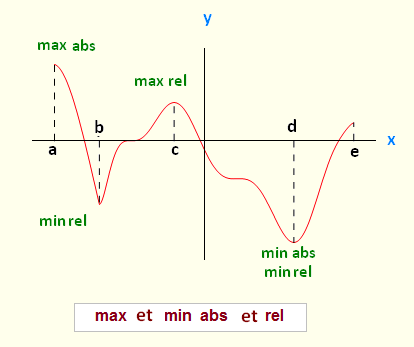
Définition
f(x) possède :
1. un maximum absolu en x = c si f(x) ≤ f(c) pour chaque x dans le domaine considéré.
2. un maximum relatif en x = c si f(x) ≤ f(c) pour chaque x dans un certain interval ouvert
autour de x = c .
3. un minimum absolu en x = c if f(x) ≥ f(c) pour chaque x dans le domaine considéré.
4. un minimum relatif en x = c x = c if f(x) ≥ f(c) pour chaque x dans un certain interval ouvert
autour de x = c .
On dit absolu ou global, relatif ou local.
|
|