Analyse
ses théorèmes
L'Analyse
Les fonctions
Continuité
Dérivabilité
Différentiabilité
Théorème des valeurs extrêmes
Théorème des valeurs intermédiaires
Théorème de la moyenne
Théorème de Rolle
Théorème de la moyenne généralisé
Théorème de Fermat
Théorème de L'Hospital
Encadrement d’une valeur
Méthode de balayage
© The scientific sentence. 2010
|
Mathématiques 3: Analyse
Variation des fonctions
Fonctions de référence
Les fonctions de référence
1. La fonction identité
Définition :
La fonction identité est la fonction f définie sur
R par
f(x) = x .
Propriété :
La fonction identité est strictement croissante sur R
2. La fonction carré
Définition :
La fonction carré est la fonction f définie sur R par
f(x) = x2 .
Propriété :
La fonction carré est strictement décroissante sur l’intervalle
]- ∞ ; 0] et strictement croissante sur l’intervalle [0; + ∞[
3. La fonction inverse
Définition :
La fonction inverse est la fonction f définie sur R \{0}
par
f(x) = 1/x .
Propriété :
La fonction inverse est strictement décroissante sur l’intervalle
]- ∞ ; 0] et strictement décroissante sur l’intervalle [0; + ∞[
4. La fonction racine carrée
Définition :
La fonction racine carrée est la fonction f définie sur
[0; + ∞[
par
f(x) = √x .
Propriété :
La fonction racine carrée est strictement croissante sur l’intervalle
[0; + ∞[
5. La fonction valeur absolue
Définition :
La fonction valeur absolue est la fonction f définie sur
R
par
f(x) = |x| .
Propriété :
La fonction valeur absolue est strictement décroissante sur l’intervalle
]- ∞ ; 0] et strictement croissante sur l’intervalle [0; + ∞[.
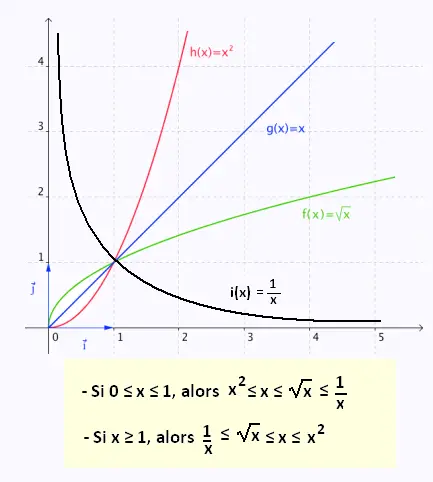
6. Ordre des fonctions de référence
|
|