Analyse
ses théorèmes
L'Analyse
Les fonctions
Continuité
Dérivabilité
Différentiabilité
Théorème des valeurs extrêmes
Théorème des valeurs intermédiaires
Théorème de la moyenne
Théorème de Rolle
Théorème de la moyenne généralisé
Théorème de Fermat
Théorème de L'Hospital
Encadrement d’une valeur
Méthode de balayage
© The scientific sentence. 2010
|
Mathématiques 3: Analyse
Variation des fonctions
Limite d'une fonction en un point
Dérivabilité
Nombre dérivé
1. Limite d'une fonction en un point
Définition :
On dit que f (x) a pour limite L lorsque x tend vers xo si les valeurs
de f(x) peuvent être aussi proche de L que l'on veut pourvu que x soit suffisamment
proche de xo.
On note :
lim f(x) = L
x → xo
La limite de f(x) lorsque x tend vers xo est égale à L.
2. Dérivabilité
2.1. Coefficient directeur d'une droite
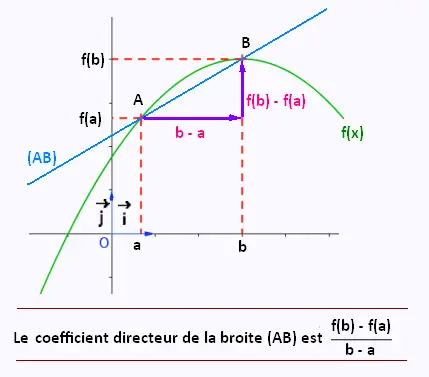
Soit une fonction f définie sur un intervalle I.
Soit deux réels a et b appartenant à I tels que a < b.
Soit A et B deux points de la courbe représentative de f d'abscisses
respectives a et b. Le coefficient directeur de la droite (AB) est égal
à :
(f(b)- f(a))/(b - a) .
2.2. Fonction dérivable
Soit une fonction f définie sur un intervalle I.
Soit un réel a appartenant à I.
Soit A et M deux points de la courbe
représentative de f d'abscisses respectives
a et a+h, avec h ≠ 0.
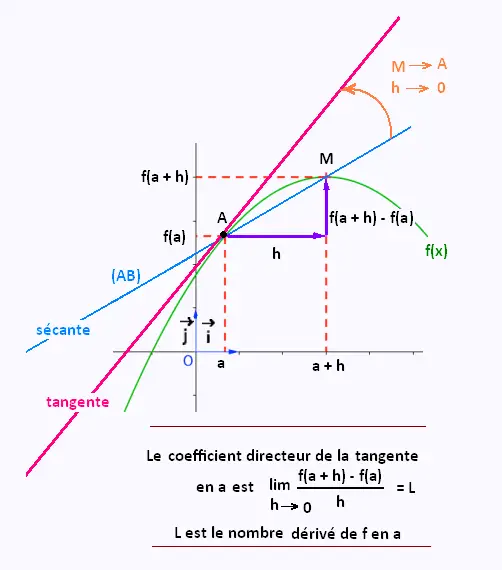
Le coefficient directeur de la droite (AM) est
égal à : (f(a + h) - f(a))/ (a + h - a) = (f(a + h) - f(a))/h .
Lorsque le point M se rapproche du point A,
le coefficient directeur de la droite (AM) est
égal à la limite de (f(a + h) - f(a))/h lorsque h
tend vers 0.
Ce coefficient directeur s'appelle le nombre
dérivé de f en a.
C'est aussi:
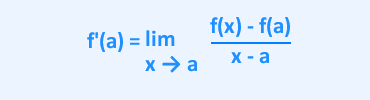
Définition :
La fonction f est dérivable en a s'il existe un nombre réel L, tel que :
lim (f(a + h) - f (a))/h = L .
h → 0
L est appelé le nombre dérivé de f en a.
3. Tangente à une courbe
Soit une fonction f définie sur un intervalle I, et dérivable en un nombre réel a
appartenant à I.
L est le nombre dérivé de f en a.
A est un point d'abscisse a appartenant à la courbe représentative Cf de f.
Définition :
La tangente à la courbe Cf au point A est la droite passant par A de
coefficient directeur le nombre dérivé L
Propriété :
Une équation de la tangente à la courbe Cf en A est :
y = L(x - a) + f (a)
Exemple :
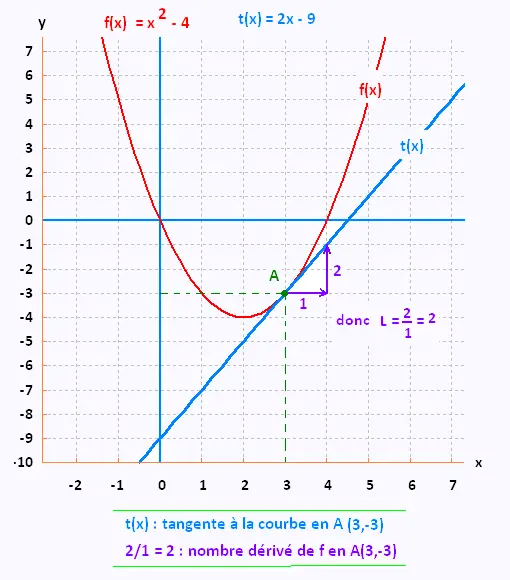
L'équation de la courbe Cf est f(x) = x2 - 4x.
Le nombre dérivé L de f en A s'obtient, après 1 unité à droite à partir du point A,
de comptant le nobre d'uniés pour rejoindre la droite tangente.
L = 2/1 = 2.
t(x) = 2(x - 3) + f (3)
D'où : f(3) = 32 - 4x3 = - 3.
Donc t(x) = 2(x - 3) - 3 = 2x - 9
L'équation de la tangente à la courbe Cf en A(3, - 3) est donc :
t(x) = 2x - 9
|
|