Analyse
ses théorèmes
L'Analyse
Les fonctions
Continuité
Dérivabilité
Différentiabilité
Théorème des valeurs extrêmes
Théorème des valeurs intermédiaires
Théorème de la moyenne
Théorème de Rolle
Théorème de la moyenne généralisé
Théorème de Fermat
Théorème de L'Hospital
Encadrement d’une valeur
Méthode de balayage
© The scientific sentence. 2010
|
Mathématiques 3: Analyse
Théorème de la moyenne généralisé
Théorème des accroissements finis généralisé
Théorème de Lagrange généralisé
Théorème de Cauchy
Théorème de la moyenne généralisé
Théorème de Cauchy
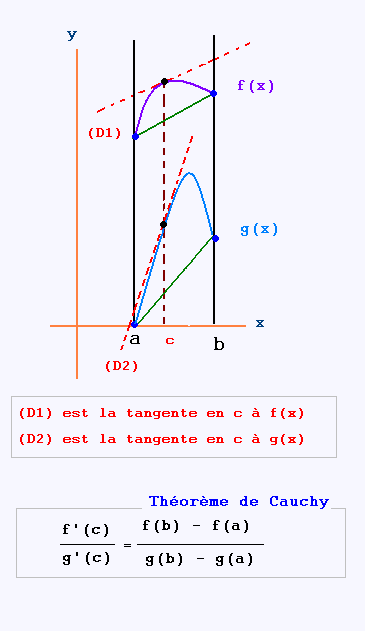
Soit deux fonctions f(x) et g(x) sont continues
sur [a,b] et sont dérivables sur ]a, b[.
Si g'(x) différent de zéro sur ]a, b[, alors
il existe au moins un réel c de l'intervalle ]a, b[ tel que:
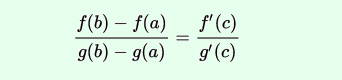
• Ce théorème peut être utilisé pour démontrer la règle de L'Hospital.
|
|