Analyse
ses théorèmes
L'Analyse
Les fonctions
Continuité
Dérivabilité
Différentiabilité
Théorème des valeurs extrêmes
Théorème des valeurs intermédiaires
Théorème de la moyenne
Théorème de Rolle
Théorème de la moyenne généralisé
Théorème de Fermat
Théorème de L'Hospital
Encadrement d’une valeur
Méthode de balayage
© The scientific sentence. 2010
|
Mathématiques 3: Analyse
Théorème de L'Hospital
La règle de L'Hospital
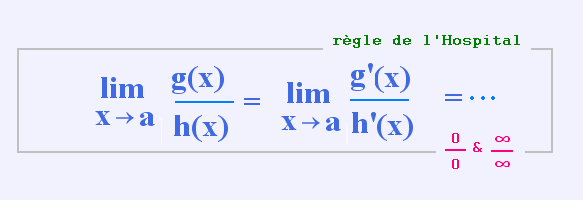
Soit f(x) = g(x) / h(x)
.
Nous voulons calculer
lim f(x)
x → a
Voici les étapes:
• 1. On commence par remplacer tous les x par la valeur a dans la fonction f(x).
• 2. Si on obtient 0/0 ou ∞/∞,
alors on dérive le numérateur g(x), puis on dérive le dénominateur h(x) pour obtenir g'(x)/h'(x).
• 3. Maintenant on applique de nouveau le point 1., en remplaçant tous les x par la valeur a dans g'(x)/h'(x).
Si on obtient un nombre réel, l'infini ou zéro, nous avons la réponse, le calcul est terminé. Sinon on passe au point 4.
• 4. Si on obtient de nouveau 0/0 ou ∞/∞ alors il faut à nouveau dériver le numérateur et le dénominateur, puis remplacer tous les x par la valeur a, et refaire les étapes qui s'en suivent jusqu'à ce que l'on obtienne un nombre réel, l'infini ou zéro.
La règle de l'Hôpital peut s'appliquer plusieurs fois de suite, jusqu'à ce que vous obteniez une réponse différente de 0/0 ou de ∞/∞.
Elle peut s'ecrire sous la forme suivante :
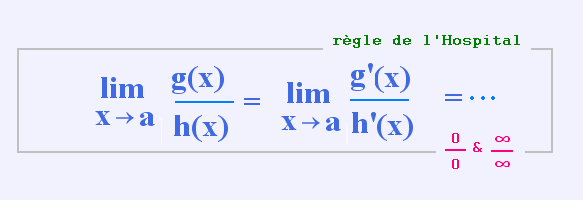
|
|