Analyse
ses théorèmes
L'Analyse
Les fonctions
Continuité
Dérivabilité
Différentiabilité
Théorème des valeurs extrêmes
Théorème des valeurs intermédiaires
Théorème de la moyenne
Théorème de Rolle
Théorème de la moyenne généralisé
Théorème de Fermat
Théorème de L'Hospital
Encadrement d’une valeur
Méthode de balayage
© The scientific sentence. 2010
|
Mathématiques 3: Analyse
Théorème des valeurs extrêmes
Théorème des valeurs extrêmes
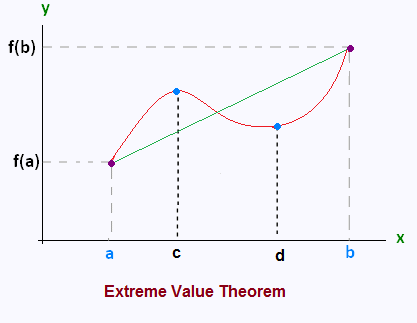
Si une fonction f(x) est continue sur un interval fermé [a, b],
alors elle a certainement un minimum absolu ET un maximum
absolu sur cet interval.
Autrement dit:
Si f est continue sur [a, b], alors il existe c et un d
dans [a,b] tels que: f(c) ≤ f(x) ≤ f(d) pour tout x
dans [a,b] .
En d'autres mots:
Si une fonction f(x) is continue sur un interval [a, b], alors
Il y a deux nombres a ≤ c, d ≤ b tels que f(c) et f(d)
sont des extrema absolus de la fonction.
|
|