Buoyant Forces

1.Pressure

Pressure is the force that is exerted on a unit surface area. It is defined as the dot product of the vector force and the vector normal to the surface. P = F . n = |F| |n| cosθ = |F| cos θ.
θ is the angle between the vector n and F. Since |n| = 1, we have then:
P = |F| cos θ.

Notice that only the component of the force , that is perpendicular to the surface exerts a pressure on this surface. Only normal force exerts a pressure.

Pressure is a scalar quantity, so it has no direction. Its SI unit is the Pa (Pascal) = 1 Newton/m²(N/m²).

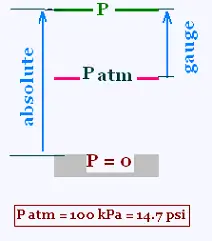
The absolute pressure is measured from zero. That is, if we press something, we just add a pressure above the already existing pressure called the atmospheric pressure. The added pressure is called gauge pressure. This added pressure is relative to the ambient atmospheric pressure.

2. Pascal's Principle

It states:

When a pressure is applied to an enclosed incompressible fluid, this pressure is fully transmitted to every point of the fluid, including the walls of the container where the fluid is confined.

3.Archimedes' principle

It states:

When an object is immersed in a fluid, the object is buoyed up by a force that is equal to the weight of the fluid displaced by this object.

4. Column height pressure

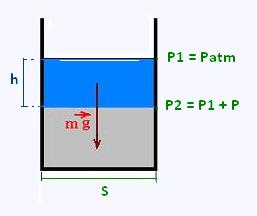
At the top, the absolute pressure P1 is equal to the atmospheric pressure Patm.
At the level h, the absolute pressure P2 is equal to the pressure Patm plus the contribution P of the column fluid of height h. Therefore: P2 = Pa + P
Where:
P is the pressure of the weight of liquid corresponding to the height h; that is P = F/S = mg/S = ρ V g/S = ρ gh

5. Buoyant force

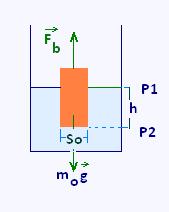
5.1. Archimedes' law

The buoyant force replaces the normal force of contact if an object was at rest on a rigid support. Here, the rigid support is replaced by an incompressible fluid.

The buoyant force is due to the difference between the pressure at the bottom surface and the pressure at the top surface. Thus:

F_b/S_o = P₂ - P₁ = P = ρ_f g h        (1)

Where
S_o is the area of the object at the bottom,
ρ_f is the density of the fluid.

We have:
V_f = h S_oV_f the volume of the displaced fluid.

If m_f is the mass of fluid displaced, then:
m_f = ρ_f V_f

Therefore:
m_f = ρ_f h S_o

If W_f = is the weight of the displaced fluid, then:
W_f = m_f g = ρ_f g V_f = ρ_f g S_o h = F_b Then: F_b = W_f = ρ_f g h S_o = ρ_f g V_f

The buoyant force is equal to the weight of the fluid's displaced volume.

5.1. Immersed object

Let's denote by h_o, V_o, m_o, and ρ_o the height, the volume, the mass, and the density of the object respectively, we have:

F_b = S_o ρ_f g h_o
V_o ρ_f g
m_o = ρ_o V_o

The object is at rest. According to the Newton's first law, we have:
F_b = m_o g

According to (1)
F_b = ρ_f g h S_o

Therefore:
m_o g = ρ_f g h S_o
That is:
ρ_o V_o g = ρ_f g V_f

Hence:
ρ_o V_o = ρ_f V_f

5.2. Wholly immersed = totally submerged body

For this case, the volume of fluid displaced is equal to the entire volume of the object.
ρ_o V_o = ρ_f V_o
or
V_o (ρ_o - ρ_f ) = 0

5.3. Does the object sink or float ?

At a certain level, when the object is wholly immersed (V_o = V_f), if we release the object we will have two cases:

1. F_b > mg:

ρ_f V_f > ρ_o V_o That is with V_f = V_o:
ρ_f > ρ_o
So, the object raise to the surface and floats.

2. F_b < mg:

ρ_f < ρ_o
The object falls to the bottom and sinks.