Les forces
Les types de forces
Le dynamique
des forces
© The scientific sentence. 2010
| Gravitational potential energy
1. Gravitational force
When an object is close to earth's surface, the gravitational potential energy
of an object of mass m at the height y from the surface is:
U(y) = m g y
For an object such as a satellite, far from the earth, another expression
for the gravitational potential energy is needed.
Newton's law of universal gravitation relates the attractive force of
interaction of two objects of mass M and m distant at r from each other center.
The magnitude of this force is:
F = G M m /r2
2. Work done by the gravitational force
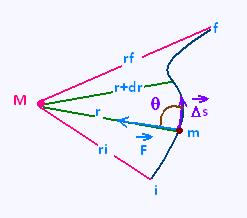
dr = Δs cos(π - θ) = - Δs cosθ
Taking any path from i to f, the gravitational force exerted on the
object of mass m does an elementary work ΔW when the position vector
changes with Δr. The object of mass m moves with respect to the
second object of mass M. The force is directed along the line joining
the two objects.
For a small displacement Δs corresponding to Δr = Δs cos θ, we have:
ΔW = F . Δs = |F| |Δs| cos θ = - F Δr
Notice that the gravitational force is conservative, the work done by
this force does not depend on path. This feature is set by the fact that
the perpendicular component of the force does not do work.
The total work done from i to f is:
W = ∫ dW = ∫ - F dr = ∫ - (G M m /r2) dr =
from ri ti rf
= - G M m ∫ dr/r2 = - G M m [-1/r] = G M m /r
from ri ti rf
W = G M m (1/rf - 1/ri)
W = G M m (1/rf - 1/ri)
3. Gravitational potential energy
The change in gravitational potential energy Uf - Ui is the negative of the work done
by the gravitational force on the object, that is:
Uf - Ui = - G M m (1/rf - 1/ri)
The convenient choice to determine the expression of the potential energy is to set it
zero when the separation is infinity, so U(∞) = 0.
Therefore:
Ug (r) = - G M m/r
Gravitational potential energy
Ug (r) = - G M m / r
4. Example: Satellite on a circular orbit
If the object of mass m is a satellite orbiting the earth of mass me, at the speed v, and
the only force that act on the satellite is the gravitational force, writing the
conservation of mechanical energy gives;
E + K + U = (1/2)m v2 + (- G mem/r)
As r increases, the potential energy increases, then the kinetic energy
decreases. Closer to the earth, the satellite moves rapidly.
For the special case of a circular orbit, the potential energy remains constant, so
the kinetic energy is. The centripetal force is provided by the gravitational force.
Newton's second law for the satellite, ΣF = m a gives:
mv2 /r = G me m /r2
Therefore:
v2 = G me/r
The kinetic energy is:
K = (1/2) mv2 = (1/2) G me m /r = - (1/2) U
In magnitude the kinetic energy is one-half the potential energy
E = K + U = - (1/2) U + U = (1/2) U
E = - (1/2) G mem /r
Total energy of the satellite of mass m
E = - (1/2) G mem /r
5. Escape speed
The mechanical energy of the satellite is negative. It due to the fact that
U is negative and the fact that U = 0 at the infinite separation of the two objects.
We can never be beyond infinity to have this energy positive, so this energy is never
positive. At least it is equal to zero once the satellite approaches infinity.
The kinetic energy is always positive.
As r approaches infinity, U approaches zero, that is the minimum value that
can take the potential energy U, the kinetic energy approaches zero as well
but still positive, so K is positive and E = U + K is positive. In other
expressions, a free object (U = 0) has more energy than the satellite has, we
say that the satellite is bounded to the earth.
The minimum required energy to free the
satellite of earth's influence is called the binding energy. For the satellite
on a circular orbit about the earth, at the position r, it is |E| = Eb = (1/2) G mem /r.
Suppose we give an object of mass o at the distance ri from the earth's surface, a speed vi.
Its kinetic energy is K = (1/2) movi2 and potential energy
U = - G me mo/ri , so its mechanical energy is:
E = K + U = (1/2) movi2 - G me mo/ri
At the infinity, the object will be free with at least 0+ kinetic energy, so
let's write at the infinity, E = 0. Therefore:
(1/2) movi2 - G me mo/ri
and
(1/2) vi2 = G me /ri
or
vi = [2 G me/ri]1/2
That is the escape speed. It doesn't depend on the mass of the
escaping object.
Escape speed
vi = [2 G me/ri]1/2
|
|