Kepler's laws

1. Introduction

The scientific interpretation of planetary motion was stared by Nicolaus Copernicus (1473 - 1543). Although a sun-centered or heliocentric model of the solar system had been proposed by Aristarchus in the third century B.C., for many centuries, one believed that the earth remains fixed while the sun and planet circle it. Copernicus remarked that this earth-centred, or geocentric model didn't correspond to the observed motion of the planets. He proposed a system where the earth rotates in its axis once per year, the earth and the other planets revolve around the sun, and the stars are at greater distance from the earth than are the sun and the planets.

Tycho Brahe (1546 - 1601) spent the last half of his life, more that twenty years, precisely measuring the position of the sun and the planets. At the end, Brahe acquired Johannes Kepler as his assistant.

Johannes Kepler (1571 - 1630) used his great mathematical ans computational abilities, and Brahe's measurements to determine the orbits of the planets, especially those of the earth and Mars. He condensed his findings into three empirical laws:

2. The three Kepler's laws

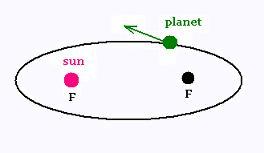1. All planets move in elliptical orbits with the sun at one focus.

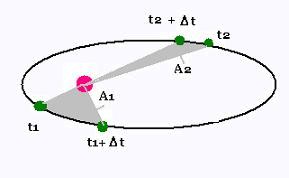
2. The motion of planets occurs in a plane, and the area swept out by the line from the sun to a planet is maintained at constant rate (equal areas in equal time intervals)

3. The square of the period of any planet is proportional to the cube of the planet's average distance from the sun.

3. Kepler's second law

This Kepler' second law can be found using Newton's second law the Newton's law of universal gravitation applied to a planet in a circular orbit.

Newton's second law applied to planet gives &Sigma F_sp = m_p a_c, where F_sp is the magnitude of the force on the planet by the sun, m_p is the mass o of the planet, and a_c is the magnitude of the centripetal acceleration of the planet around the sun.

Since F_sp = G m_s m_p/r², and a_c = v²/r = (ωr)²/r = ω² r
= (2π/T)² r = 4 π² r/T², T is the period of revolution of the planet about the sun.

Therefore:
4 m_p π² r/T² = F_sp = G m_s m_p/r², That is:
T² = (4 π²/G m_s) r³

4. Kepler's third law

This Kepler' third law can be found using again Newton's second law and Newton's law of universal gravitation applied to a planet.

Kepler's third law states: The motion of planets occurs in a plane, and the area swept out by the line from the sun to a planet is maintained at constant rate.

Therefore:

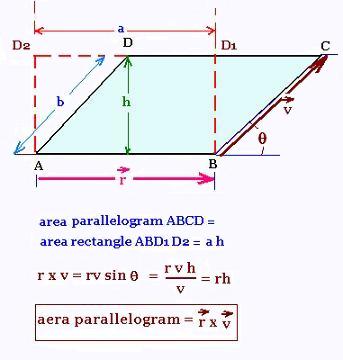
The area element ΔA swept in the time interval Δt is:
ΔA = (1/2) r Δr (the half of the parallelogram of area r Δr) = |(1/2) r x Δr|
At the limit as Δ → 0
dA = (1/2) |r x dr|

Since dr = v dt, we obtain:
dA = (1/2) dt |r x v|, or dA/dt = |r x v|

According to Kepler's third law, this rate is constant that is the cross product r x v is constant vector. Therefore, this cross product vector is normal to the plane of motion that contains r and v.

The derivative of the cross product gives:
d(r x v)/dt = 0 . That is:



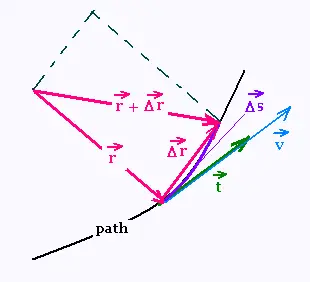
d(r x v)/dt = (dr/dt) x v + r x dv/dt =
v x v + r x a = r x a = 0

r x a = 0 means that the acceleration a is parallel to the position r vector.

This acceleration multiplied by the inertial mass m gives, according to Newton's second law, the related force which is the only force applied to this mass. So this centripetal force is parallel to r; and according to Newton's law of universal gravitation, this centripetal force is provided by another force which is the gravitational force.