Resultant force
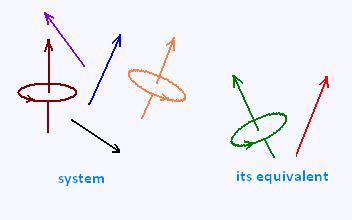
When a system of several forces and several couple moments are acting on a rigid body, we can replace all of them by a unique force and unique couple momemt, at a certain point, that will have the same overall external effect on the body. The obtained force and couple moment are called equivalent system.
1. Moving a force on its line of action
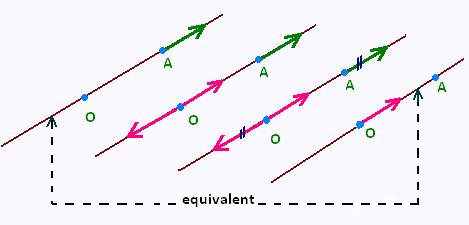
Since the body is rigid, moving a force along with its line of action, from the point A to the point O, which both are on the vector's line of action, does not change the external effect. Therefore this force vector is called a sliding vector. There is an internal effect within the body due to the force, that depends indeed on where this force is applied.
2. Moving a force of its line of action
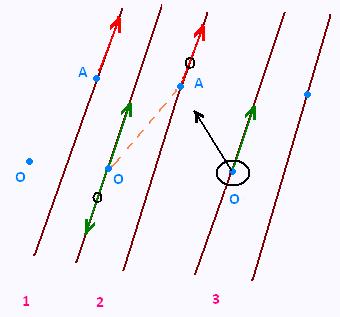
Moving a force out off its line of action, from the point A to the point B, which both are not on the vector's line of action, does not change the external effect. Therefore this delocalized force is accompanied with a brand new couple moment. This moment is a free vector and can be applied at any point on the body.
3. Resultant force and resultant moments of a system
With several forces and their couple moments acting on a body, he rule is to move each force and its associated couple moment to a common point, and find the resultant force-couple moment. Therefore The total force is the sum of all the forces, and the total moment is the sum of the generated couple moments Mcg and the moments non generated Mng by the forces:
At the common point:
FR = ΣF
MRO = ΣMcg + ΣMng
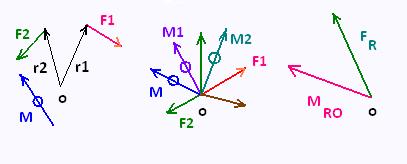
Each force Fi comes to the point O and remains Fi plus a couple momemnt:
Mi = ri x Fi
FR = ΣFi
MRO = ΣMgi + ΣMngi
4. Reducing a force and couple system to a single force
If the resultant force and the resultant couple are perpendicular,
then we can find an equivalent system with a single force
and no couple.
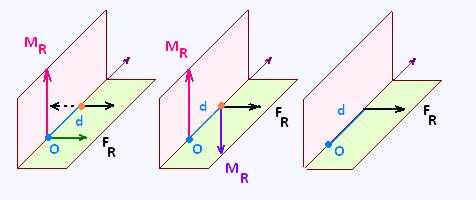
To obtain this system, we move the resultant force a distance d
along the line perpendicular to the plane of the resultant force and
resultant couple until the resultant force creates a moment
equivalent to the resultant couple: d = MR/FR
5. Independence of reference point: Free vector
Unlike the moment of a force that is always defined with respect to a certain
reference point, the moment of a couple is independent of
the reference point, hence it is a free vector.
Proof:
If we have a couple of force vectors F1 and F2, that form
tho couple moments M1 and M2 with position vectors from
a certain point r1 and r2, respectively. The couple
moment about this point is:
M = M1 + M2 =
r1 x F1 + r2 x F2.
Since F1 = - F2 = F, we get then:
M = (r1 - r2)x F.
The difference r1 - r2 is not a position vector, it is independent of point of reference.
Recall:
The couple moment is a free vector.
6. Example
The rule is to:
- Sum all the x-components and y-components of the force to find the equivalent single force FR,
- Sum all the moments with respect to the reference point O to finf the resultant moment MRO , and
- Find the location of FR, that is the distance d from the point O:
d = MRO /FR
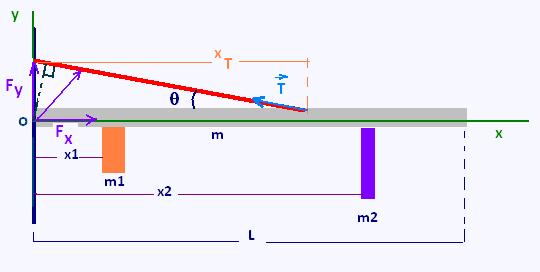
A pivoted uniform boom with a cable is in equilibrium. The pivot at the wall exerts no torque.
The forces exerted on the boom lie in the x-y plane. These force are obtained using the scalar following equations:
FRx = ΣFix
FRy = ΣFiy
MRO = ΣMgi
then obtainable from the force equation shown. The lever arm for the cable tension T must be obtained from the triangle as shown since the cable is not perpendicular to the boom.
Fx = 10 N, Fy = 12 N, T = 4 N
θ = 30o
m1 = 2 kg, m = 1 kg, m2 = 3 kg
L = 4 m, x1 = 1 m, x2 = 3 m, xi = 2.5 m
1. The expression of the resultant force:
FRx = ΣFix =
FRx = Fx - T cos θ
= 10 - 4 cos 30o = 6.54 N
FRy = Fy + T sin θ -m1 g -m g - m2 g
= 12 + 4 sin 30o - (2 + 1 + 3) 9.81 = - 44.90 N
F = [ FRx2 + FRy2]1/2 = 45.40 N
tg φ = -44.90/6.54 = -6.85
φ = - 82o
1. The expression of the resultant moment:
We choose the point pivot O as the reference point, then:
MRO = ΣMgi =
m1 x1 + m L/2 + m2 x2 - T sin θ xT
= 1 x 1 + 1 x 2 + 3 x 3 - 4 (1/2) x 2.5 = 7 N.m
d = 7/45.40 = 0.15 m = 15.0 cm
|