Méchanique:
Vecteurs
1. Définitions
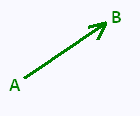
On apelle vecteur un segment de droite orienté noté
. A est
l'origine du vecteur et B son extrémité.
On distingue trois types de vecteurs: vecteurs libres, glissants et liés.
Vecteur libre :
Un vecteur libre est défini par sa direction, son sens et sa valeur, son point d’application (origine) pouvant être quelconque dans l’espace.
Exemple : le vecteur de l’accélération de la pesanteur est un vecteur libre.
Vecteur glissant:
Un vecteur glissant est défini par sa droite d’action (support), son sens et sa valeur, son point d’application pouvant être quelconque sur la droite d’action.
Exemple: Une force appliquée à un solide indéformable peut glisser sur sa droite d’action sans modifier l’effet qu’elle produit. On dira que la force est représentée par un vecteur glissant.
Vecteur lié:
Un vecteur lié est défini par sa droite d’action son sens, sa valeur et son point d’application.
Exemple : Le poids d'un corps est un vecteur lié. C'est un vecteur qui a un point d’application bien défini qui est le barycentre ou le centre de gravité du corps.
• On peut remplacer un vecteur libre par un vecteur équipollent quelconque, dans tout l'espace.
• On peut glisser un vecteur glissant le long de son support.
• Un vecteur lié ne peut pas être remplacé par un autre vecteur.
Résumé
On distingue les vecteurs liés, glissants et libres comme suit:
• Un vecteur lié a un point d’application bien défini.
• Un vecteur glissant a un point d’application variant sur une droite qui est son support.
• Un vecteur libre a un point d’application quelconque.
Deux vecteurs sont équipollents (ou égaux) s'ils ont même direction
(ou même support), même sens et même valeur.
Deux vecteurs sont colinéaires (parallèles) s'ils ont même direction
(ou même support) et des valeurs proportionnelles.
Autrement dit, deux vecteurs sont colinéaires si et seulement si l’un est un multiple de l’autre.
Des vecteurs sont dits linéairement dépendants si l’un est
une combinaison linéaire des autres. À l'inverse, ils sont dits linéairement indépendants.
|