Calculus I:
Functions of several variables
Extrema of a single variable function

Extrema of a single
variable function

We know how to find and study the maximum and the minimum of a function of one variable.

For this we use the derivative. We will see in this chapter how to find the maximum or the minimum of a function of several variables.

Let's start with the case of a single variable.


Definition

Let f be a function defined over an interval I and xo I.

1. f(x0) is a global (absolute) maximum of f if:
f (x) = f (x0), for all x I.

2. f (x0) is a local maximum of f if there is an interval] ]a, b [ I containing x0 such as:
f (x) = f (x0), for all x ] a, b [.

3. f (x0) is an global minimum of f if:
f (x) = f (x0), for all x I.

4. f (x0) is a local minimum of f if there is an interval] a, b [ I containing x0 such as:
f (x) = f (x0), for all x ] a, b [.

An extremum (plural extrema) means either a maximum or a minimum.


Exercise 1

Graphically, give the local and global extrema of the function f defined in [0, 3.5]:



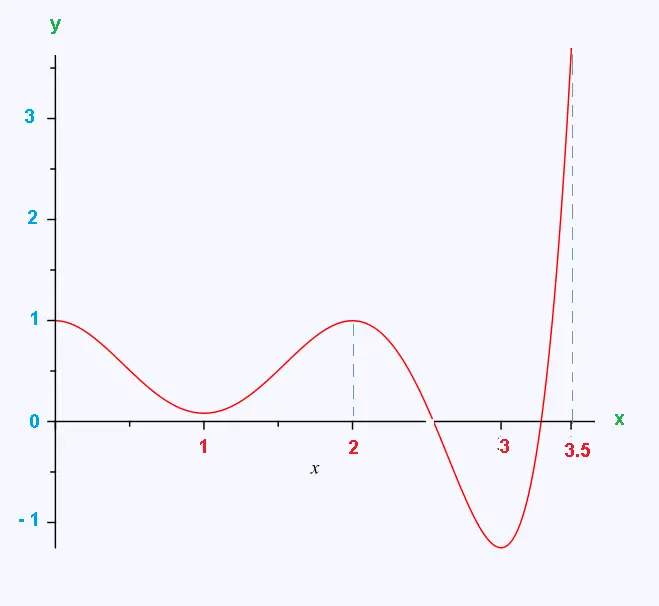
Solution:

On the graph we find that

in x = 0 and x = 2 we have a maximum local,
in x = 1 we have a local minimum,
in x = 3 we have a global maximum overall and
in x = 3, 5 we have an global maximum.

To detect local extrema we have the following property:


Proposition

If f has a relative extremum in x = xo then let f'(xo) = 0 either f'(x0) does not exist.


Exercise 2

1. Show that the function f (x) = x2 + 7 has a global minimum in x = 0.

2. Show that the function f (x) = x2 is defined on [-1; 1] admits a global maximum in x = -1.

3. Show that the function f (x) = |x| + 2 has an global minimum of x = 0.

Solution:

1. We have f'(x) = 2x. The function f' is defined in R and is null when x = 0. So if f admits a local extremum then it is in x = 0.

Since we have f (0) = 7 = x2 + 7 = f (x), we deduct that we have a global minimum.

2. If -1 = x = 1 then x2 = 1. We have f (x) = f (1) for x [-1; 1].

So the function studied has a maximum in x = 1.

We notice that at x = 1 the derivative of the function studied does not exist. Indeed, by definition:

f'(1) = lim (f (1 + h) - f (1))/h
h → 0

This supposes that f (1 + h) exists when h> 0, but here f is defined only on [-1; 1], so f'(1) does not exist.

3. Here is the graphical representation of f


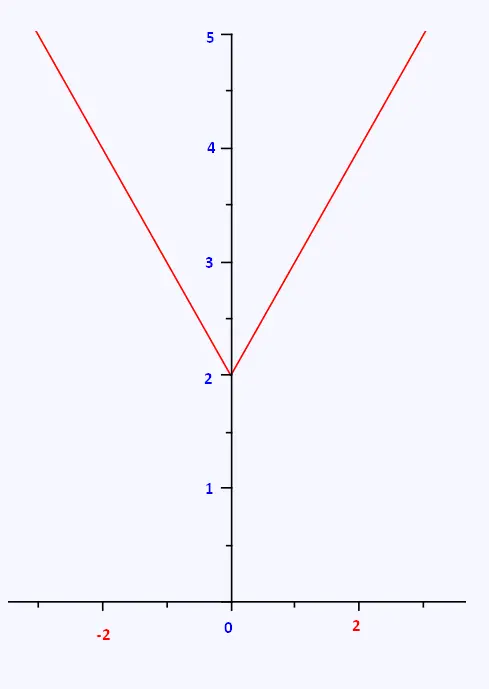
Figure Graphical Representation of f (x) = | x | + 2.

We have f'(x) = -1 when x < 0 and f'(x) = 1 when x > 0.

The function f' is not defined when x = 0. So if f admits a local extremum then this one is in x = 0. Like, we have f (0) = 2 = | x | + 2 = f (x), we deduce that we have a global minimum.


Exercise 3

Let f be the function defined on R by f (x) = x3. Does this function admit an extremum ?

Solution:

We have f'(x)= 3x2. The derivative is defined on R and f'(x) = 0 when x = 0.

So, if we have an extremum then it is in x = 0.

Now, f(x) = x3 = 0 = f (0) for x = 0 and f (x) = x3 = 0 = f (0) for x = 0 so f does not have extremum.



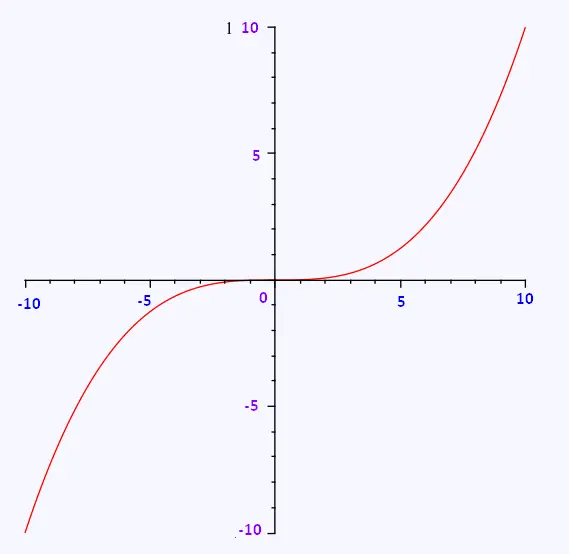
Figure 4.3 - Graphical representation of f (x) = x3.

We just saw that f'(x) = 0 is not enough to guarantee the existence of a extremum. The following property using the second derivative completes this gap.

Indeed, by studying the concavity or convexity of the function we can determine if a point is a local extremum.


Proposition 2

Let f be a function defined over an interval I and x0 I. Let ]a, b[ an interval containing x0.

We suppose that f'(x0) = 0 and that f" exists on ]a, b[ I in this case:

1. if f"(x0) > 0, then f (x0) is a local minimum.
2. if f"(x0) < 0, then f (x0) is a local maximum.


Exercise 4

Show that in x = 3 the function f (x) = -x2 + 6x - 8 admits a local maximum.

Solution:

We have f'(x) = -2x + 6, we deduce f'(x) = 0 when x = 3.

On the other hand, f"(x) = -2. So f"(3) = -2 < 0.

Thus f admits a local maximum in x = 3.


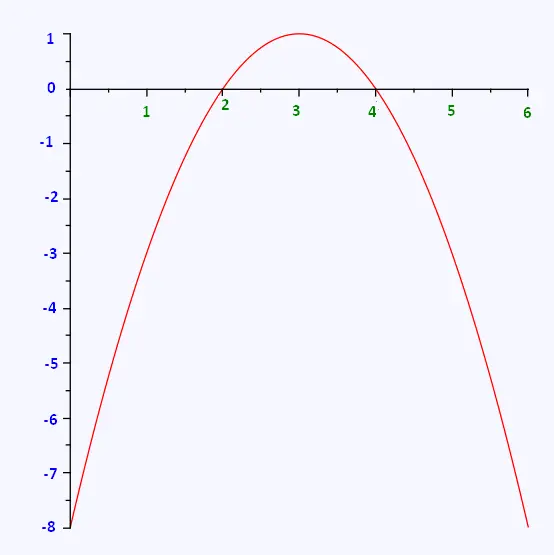
Graphical Representation of f (x) = - x2 + 6x - 8