Calculus I:
Functions of several variables
Extrema of a several variable function

Extrema of a several
variable function

We want to study the extrema of a function of several variables.

We will generalize what we know how about a single variable function.

In this course, we will study the case of the functions of two variables.

In order to reduce the definitions of maximum and minimum in the context of functions of two variables we introduce the following notion of neighborhood:

Definition 1

We call the neighborhood of a point (x0, y0) R2 any part of the plane containing a disc of center (x0, y0) and of strictly positive radius.

We can notice that a part of the plane is a neighborhood of a point when this point is placed within this part. In other words, a set is not a neighborhood of a point when the point is not in that set or when the point is on the edge of the considered set.

Definition 2

Let f be a function of two variables x, y defined on a part D R2 and (x0, y0) D.

1. f (x0, y0) is an global maximum of f if:
f (x, y) ≤ f (x0, y0), for all (x, y) D.

2. f (x0, y0) is a local maximum of f if there is a neighborhood V D of (x0, y0) such as :
f (x, y) ≤ f (x0, y0), for all (x, y) V.

3. f (x0, y0) is an global minimum of f if:
f (x, y) ≥ f (x0, y0), for all (x, y) D.

4. f (x0, y0) is a local minimum of f if there exists a neighborhood V D of (x0, y0) such as :
f (x, y) ≥ f (x0, y0), for all (x, y) V.

To detect local extrema we have the following property:

Proposition 1

If f has a relative extremum in (x0, y0) then:

• ∂f/∂x (x0,y0) = 0
and ∂f/∂y (x0,y0) = 0

or

• either one of the partial derivative ∂f/∂x , ∂f/∂x does not exist.

A point (x0, y0) satisfying one of these conditions is called a critical point.

Exercise 1.

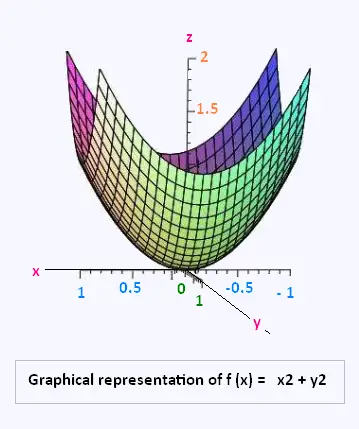
Show that the function f(x, y) = x2 + y2 has a local minimum in (0; 0).

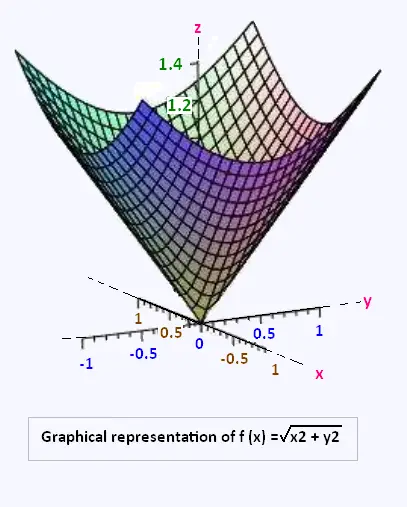
2. Show that the function f(x, y) = √(x2 + y2) has a local minimum in (0; 0).

Solution:

1. We have ∂f

∂f/∂x (x,y) = 2 x
∂f/∂x (x,y) = 2 y

We have 2x = 0 and 2y = 0 if and only if x = 0 and y = 0. So, if f admits a local extremum then it is in (0; 0).

We have f (0,0) = 0 ≥ x2 + y2 = f (x, y), since a square is positive.

We deduce that (0; 0) is a local minimum (even global).

The following figure, see Figure 4.6, gives the graphical representation of f.



2. We have

∂f/∂x (x,y) = x/√(x2+ y2)
∂f/∂y (x,y) = y/√(x2+ y2)

We have

∂f/∂x (x,y) and ∂f/∂y (x,y) (x, y) which are not defined in (0, 0) (division by zero).

Moreover, a fraction is null if and only if its numerator is zero. So to get ∂f/∂x (x,y) = 0 and ∂f/∂y (x,y) = 0, (x, y) = 0 must have x = 0 and y = 0. Now this gives us the forbidden value obtained previously.

Thus, if f admits a local extremum then it is in (0; 0).

We have f 0, 0) = 0 ≥ √(x2 + y2) = f (x, y), because a square root is positive. We deduce that f(0;0) is a local minimum (even global).

Here is the graphical representation of f:


Exercise 2.

Let f be the function defined on R by f (x, y) = x2 - y2.
Does this function admit an extremum ?

Solution:

We have

∂f/∂x (x, y) = 2x and
∂f/∂x(x, y) = - 2y.

The two partial outlines are defined on R2.

In addition, ∂f/∂x(x, y) = 0 when x = 0 and ∂f/∂y(x, y) = 0 when y = 0.

So, if we have an extremum then this one is in (0; 0).
But

• f (0; 0) = 0 = x2 = f (x, 0). So all coordinate points (x; 0) have a image above f (0; 0).

• f (0; 0) = 0 = -y2 = f (0, y). So all the points of coordinates (0; y) have an image below f (0; 0).

Conclusion: The function f does not admit extremum.

In such a situation, we say that the point (0; 0; f (0, 0)) is a saddle point.

This name is understood by means of the graphical representation of this function.
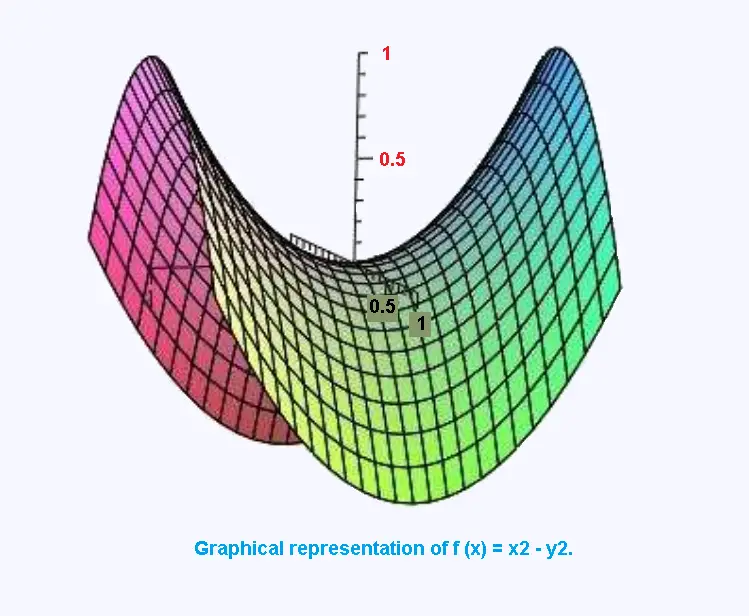
Graphical representation of f (x) = x2 - y2.

We have just seen that the condition ∂f/∂x(xo, yo) = 0 and ∂f/∂y(xo, yo) = 0

is not enough not to guarantee the existence of an extremum. As in the case of functions of single variable, we can fill this gap by studying the second derivatives.

Proposition 2

Let f be a function of two variables x, y defined on a part D ∂ R2 and (x0, y0) ∂ D verifiying ∂f/∂x(xo, yo) = 0 and
∂f/∂y(xo, yo) = 0

We write

d = ∂2f/∂x2 (x0, y0). ∂2f/∂y2 (x0, y0) - (∂2f/∂x∂y(x0, y0))2 .

1. if d> 0, and ∂2f/∂x2 (x0, y0)> 0 then f (x0, y0) is a local minimum.

2. if d> 0, and ∂2f/∂x2 (x0, y0) < 0 so f (x0, y0) is a local maximum.

3. if d < 0 then (x0, y0, f (x0, y0) is a saddle point, so f(x0, y0) is not a extremum.


Exercise 3.

Find the extrema and saddle points of the function f (x, y) = xy - (1/4)x4 - (1/4)y4.

Solution:

Here is the graphical representation of f.


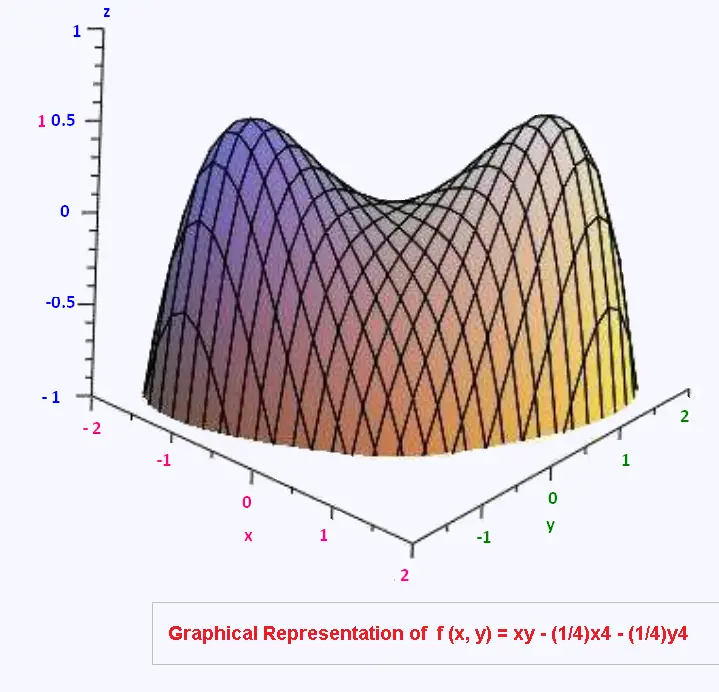
Graphical Representation of
f (x, y) = xy - (1/4)x4 - (1/4)y4.

First, let's look for the critical points of f.

We have ∂f

∂f/∂x (x, y) = = y - x3 and
∂f/∂y(x, y) = x - y3.

These two functions are defined in R2. We then seek to solve the following system:

y - x3 = 0
x - y3 = 0.

This gives:

y - x3 = 0
x - y3 = 0

y = x3
x = (x3) 3 = x9 ∂

y = x3
x9 - x = x (x8 - 1) = 0.

The last equation gives us as a possible value for x, x = 0 and the eighth roots of the unit.

But we are only looking for real roots, so the Possible values ∂∂of x are x = 0, x = 1 and x = -1.

This gives as solutions raves of the system (0; 0), (1; 1) and (-1; -1).

On the other hand, we have:

∂2f/∂x2 (x, y) = - 3x2 ,
∂2f/∂y2 (x, y) = - 3y2,
∂2f/∂x∂y(x, y) = 1.

We then obtain:

• In (-1; -1), we have d = (-3). (- 3) -1 = 8 > 0 and

∂2f/∂x2 (-1,-1) = -3 < 0, hence f (-1; -1) is a local maximum.

• In (0; 0), we have d = 0 - 1 = -1 < 0, so (0; 0; f (0; 0) is a point saddle.

• In (1; 1), we have d = (-3). (- 3) - 1 = 8 > 0 ∂2f/∂x2 (1,1) = - 3 < 0, hence f (-1; -1) is a local maximum.