Calculus I:
functions of several variables
linear approximation
Approximation of a function of a single variable

Approximation of a function
of a single variable

Once again we begin a chapter by recalling the definition of the derivative of a function in a single variable.

Definition

f: D → R
x → f (x)

We say that f is differentiable in x and of f'(x) is its derivative when the next limit is defned, that is the limit exists and it is not + ∞ or - ∞.

f'(x) = lim f(x + δx) - f (x)
δx → 0

Note :

Traditionally when we define the derivative of a function in a theoritical point of view, the small number that tends to 0 is noted h. When performing a calculation of error, we use as notation δx instead of h.

Since we have a equality when δx tends to 0, we deduct the following approximation

Proposition 1

f'(x) ≈ [f(x + δx) - f (x)]/δx

Exercise 1

Using the following table of values, give an approximation of f'(3).

x     1.5   2    3      3.2     4     5
f(x)  6     10   12.5   15.6    20    25 

Solution:

We apply the preceding formula with x = 3 and δx = 0.2. We obtain:

f'(3) ≈ [f(3 + 0.2) - f (3)]/0.2 =
[f(3.2) - f (3)]/0.2 = (15.6 - 12.5)/0.2 = 15.5

f'(3) ≈ 15.5


Since f'(x) ≈ [f(x + δx) - f (x)]/δx

we have

f'(x) δx ≈ f(x + δx) - f (x)

and therefore another way of writing the previous approximation is:


Proposition 2

Affine approximation of a function of a variable).

f(x + δx) ≈ f'(x) δx + f (x)

Graphical interpretation



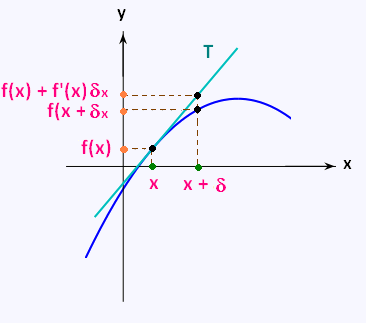
T is the tangent of f in x. With our notations f'(x) δx + f (x) represents the ordinate of the point of T of abscissa x + δx.

It is therefore natural to say that f(x + δx) and f'(x) δx + f (x) are very close.

Exercise 2

Without calculator give an approximate value of √2.05.

Solution:

We consider the following function f:
f: R+ → R+
x → √x

We are therefore looking for an approximation of f(2.05).

We put: x = 1, dx = 0, 05.
We get: √2.05 = f (2.05) ˜ f(2) + f'(2) x 0, 05.
We have: f (2) = 1.41
f'(x) = 1/(2√x), so f'(2) = 1/2x1.41 = 1/2.82.
Hence: √2.05 ˜ 1.41 + 1/2.82 x 0.05 = 1.41 + 0.0177 = 1.4277.

Conclusion: √2.05 ˜ 1.4277.

Note: The exact value of √2.05 is 1.4318 ...