Contents
ScientificSentence
© The scientific sentence. 2010
|
Optics: Applications
1. Refraction across a 30o prism
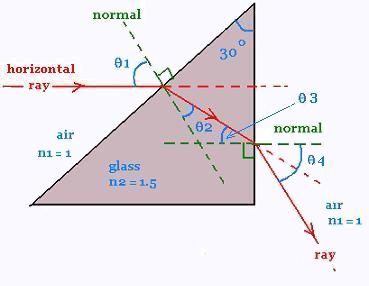
We want to find the angular displacement θ3 of the ray after having passed through the prism.
We have
θ1 = 90o - 60o = 30o
According Snell's law, we have:
1 sin θ1 = 1.5 sin θ2
Therefore
sin θ2 = (1/1.5) sin 30o = 0.333
θ2 = 19.50o
(90 - 19.50) + 30 = 180 - (90 - θ3)
(90 - 19.50) + 30 = 180 - (90 - θ3)
θ3 = 10.53
According Snell's law, we have:
1.5 sin θ3 = 1 sin θ4
1.5 sin(10.53) = sin θ4
sin θ4 = 0.27
θ4 = 15.90o
2. Brewster Angle
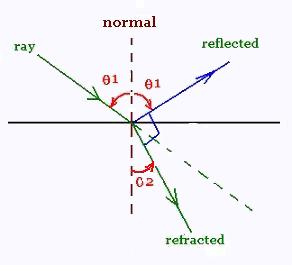
The Brewster angle is the angle of incidence that
corresponds to the reflected ray perpendicular to
the refracted ray.
We want to find the relationship between
θ1 and the two refraction indexes n1 and n2.
We have
θ1 + θ2 = 90o
According Snell's law, we have:
n1 sin θ1 = n2 sin θ2
Therefore
n1 sin θ1 = n2 sin θ2 = n2 sin (90 - θ1)
= n2 cos θ1
Hence;
tan θ1 = n2/n1
tan θ1 = n2/n1
3. Apparent depth under water
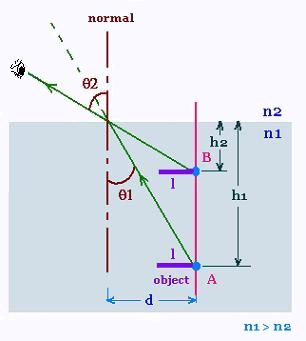
Objects under water always look shallower than they
really are. If one looks straight down into water that
is actually 4.00 m deep, how deep does it appear to be?
The surface of the water acts as a plane refracting surface.
The ray that comes from the point A in the medium
of index of refraction n1 is refracted in the upper
medium of index of refraction n2 (here n2 < n1).
If the apparent depth is h2 and the actual depth is h1,
we can write:
tan θ1 = d/h1, and tan θ2 = d/h2 , therefore
d = h1 tan θ1 = h2 tan θ2
According Snell's law, we have:
n1 sin θ1 = n2 sin θ2
Therefore
n1 cos θ1 tan θ1 = n2 cos θ2 tanθ2
Or:
n1 h2 cos θ1 = n2 h1 cos θ2
Hence:
h2 = (n2/n1) h1 (cos θ2/cos θ1)
We assume that the two angles θ1 and θ2 are
small, then their cosines are equal to 1, therefore:
h2 = (n2/n1) h1 (cos θ2/cos θ1)
h2 = (n2/n1) h1
As B, the image of the point A, is virtual, we can
write:
h2 = - (n2/n1) h1
The lateral magnification is:
m = (length of the image on B)/(length of the object on A) =
- (n1h1/n2h2) = 1.
We find then the result that the image formed by a plane refracting
surface has the same lateral size as the object.
|
|