Contents
ScientificSentence
© The scientific sentence. 2010
| Optics: Descartes' Rainbow
1. Descartes' Rainbow
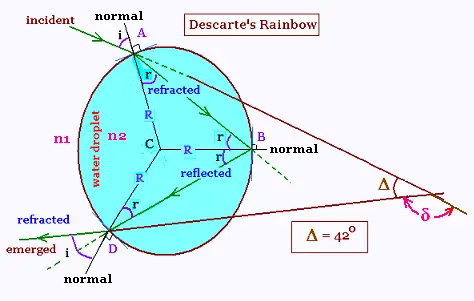
The white ray light travels from air of index of refraction n1, through a water
droplet of index of refraction n2, and emerges to the air toward an observer.
What are the colors could we see? What is the minimum deviation of the
ray?. We will use the model of Descartes to answer these two questions. We will
see the two rainbows: the primary (one internal reflection and two refractions) and
the secondary (two internal reflections and two refractions).
δ is the deviation between the incidence and emergence
of the sun light ray.
δ = (i - r) + (2π - 2r) + (i - r)
= 2π + 2i - 4r
We have Δ = 2π - δ
Δ = 2π - (2π + 2i - 4r)
Δ = 4r - 2i (1)
d(Δ)/di = d(4r - 2i)/di = 0
Then: dr/di = 1/2 (2)
From Snell's law, we have:
n1 sin i = n2 sin r ⇉ sin r = (n1/n2) sin i. The
ratio n1/n2 for air-water is generally taken equal to 3/4.
Therefore:
r = arcsin((n1/n2) sin i)
dr/di = [1 - (n1/n2)2 sin2 i]-1/2 x (n1/n2) cos i (3)
The relationship (2) becomes:
1/2 = [1 - (n1/n2)2 sin2 i]-1/2 x (n1/n2) cos i
Or
(1/4) [1 - (n1/n2)2 sin2 i] = (n1/n2)2 cos2 i
= (n1/n2)2 (1 - sin2 i)
Then:
(1/4) = (1/4) (n1/n2)2 sin2 i + (n1/n2)2 (1 - sin2 i)
= (1/4) (n1/n2)2 sin2 i + (n1/n2)2 - (n1/n2)2 sin2 i
Thus:
(1/4) - (n1/n2)2 = - (3/4) (n1/n2)2 sin2 i
or
(n1/n2)2 - (1/4) = (3/4) (n1/n2)2 sin2 i
(4/3) [(n1/n2)2 - 1/4] (n2/n1)2 = sin2 i
(4/3) [1 - (1/4) (n2/n1)2] = sin2 i
sin i = ((4/3) [1 - (1/4) (n2/n1)2])1/2
sin i = ((1/3) [4 - (n2/n1)2])1/2
i = arcsin [([4 - (n2/n1)2]/3)1/2] (4)
i = arcsin [([4 - (n2/n1)2]/3)1/2]
for n2/n1 = 4/3, we have :
i = arcsin [((1/3) [4 - 16/9])1/2] = arcsin((20/27)1/2)= 59.40
i = 59.40 o
From Snell's law: n1 sin i = n2 sin r, we have:
r = arcsin[(n1/n2) sin i] = arcsin[(3/4) (20/27)1/2] = arcsin[0.64] = 40.20
= 40.20 o
r = arcsin[(n1/n2) sin i]
The relationship (1) becomes:
Δ = 4r - 2i
Δ = 4r - 2i = 4(40.20)o - 2(59.40)o =
160.80o - 118.80 o = 42o.
Δ = 42o
Then, the deviation is :
δ = 2π - δ = 222 o
Note &delta is min, then Δ is max.
The relative index of refraction of a ray from
the medium n1 to the medium n2 is:
n = n2/n1
Thus, Snell's law is rewritten, if i and r are the angles od incidence
and refraction respectively, as:
sin i = n sin r → sin r = (1/n) sin i
Using the relationship (2): dr/di = 1/2, we get:
cos r (dr/di) = (1/2) cos r = (1/n) cos i
Thus cos i = (n/2) cos r = (n/2) [1 - sin2r]1/2 =
(n/2) [1 - (1/n)2 sin2i]1/2
= (n/2) [1 - (1/n)2 (1 - cos2i)]1/2
= (n/2) [1 - (1/n)2 + (1/n)2 cos 2i]1/2
Then:
cos2 i = (n/2)2 [1 - (1/n)2 + (1/n)2 cos2i] =
(n/2)2 - (1/4)+ (1/4) cos2i)
Or:
(3/4) cos2i = (n/2)2 - (1/4).
Hence
3 cos2i = n2 - 1. Then
cos i = [(n2 - 1)/3]1/2
cos i = [(n2 - 1)/3]1/2
2. Properties of Descartes' Rainbow
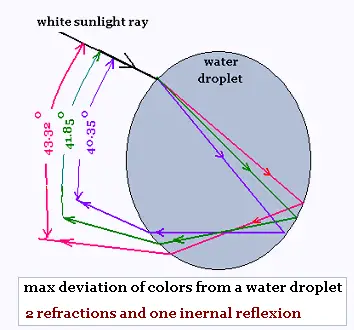 Here is a table that gives the color, the wavelength in vacuum, the
related index of refraction in water, and the related Descartes rainbow max
deviation.
Here is a table that gives the color, the wavelength in vacuum, the
related index of refraction in water, and the related Descartes rainbow max
deviation.
The index of refraction of air is taken equal to
1.0003 for all these wavelengths of the white light ray spectrum.
| color | wavelength | index of refraction | max rainbow deviation |
| violet | 380�450 | 1.3455 | 40.35 |
| blue | 450�475 | 1.3425 | 40.77 |
| green | 495�570 | 1.3350 | 41.85 |
| yellow | 570�590 | 1.3334 | 42.08 |
| orange | 590�620 | 1.3330 | 42.14 |
| red | 620�750 | 1.3250 | 43.32 |
The values of the refractive indexes in water, in this table,
are the average
values taken from the results of philip Laven .
3. Secondary rainbow
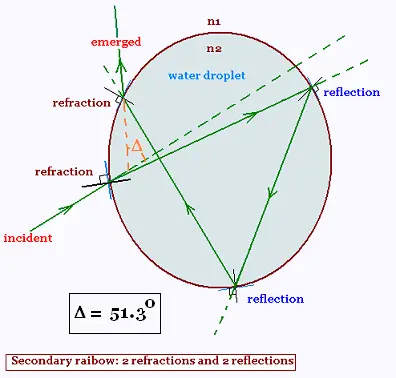
In this case have, we have two internal reflections and two
refractions:
δ = (i - r) + (2π - 2r) + (i - r) + 2π - 2r
δ = 2i - 6r + 4π
The condition of minimum is written as:
dδ/di = 0 = 2 - 6 (dr/di).
Hence:
dr/di = 1/3
Using Snell's law:
sin r = (1/n) sin i, we get:
cos r (dr/di) = (1/3) cos r = (1/n) cos i
Thus cos i = (n/3) cos r = (n/3) [1 - sin2r]1/2 =
(n/3) [1 - (1/n)2 sin2i]1/2
= (n/3) [1 - (1/n)2 (1 - cos2i)]1/2
= (n/3) [1 - (1/n)2 + (1/n)2 cos 2i]1/2
Then:
cos2 i = (n/3)2 [1 - (1/n)2 + (1/n)2 cos2i] =
(n/3)2 - (1/9)+ (1/9) cos2i = 0.
Or:
(8/9) cos2i = (n/3)2 - (1/9).
Hence
8 cos2i = n2 - 1. Then
cos i = [(n2 - 1)/8]1/2.
The condition of minimum is:
cos i = [(n2 - 1)/8]1/2
For the example of n = 4/3, we have:
i = arcos [(n2 - 1)/8]1/2 = arcos [(16/9 - 1)/8]1/2 = 72.0 o
i = 72.0 o
r = arcsin [(1/n) sin i] = arcsin [(3/4) sin 72.0] = 45.45o
r = arcsin [(1/n) sin i] = arcsin [(3/4) sin 72.0] = 45.45o
r = 45.45o
δ = 2i - 6r + 4π = 2 x 72.0 - 6 x 45.45 + 00 = 144 - 272.7 + 720 = 591.3 ==
591.3 - 360 = 231.3
Δ = δ - π = 231.3 - 180 = 51.3o
Δ = 51.3o
|
|