Contents
ScientificSentence
© The scientific sentence. 2010
|
Optics: Deviation for a prism
1. Deviation for a prism:
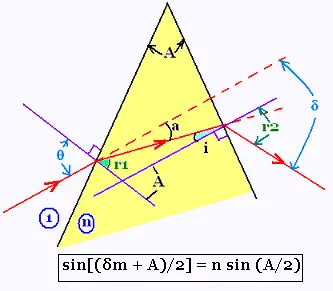
We have the five following relationships:
i + r1 = A
θ = a + r1
sin θ = n sin r1
n sin i = sin r2
δ = a + r2 - i
Then:
δ = θ - r1 + arcsin[n sin i] - i =
θ + arcsin[n sin i] - A
arcsin[n sin i] = arcsin[n sin (A - r1)] =
arcsin[n sin (A - arcsin (sin θ)/n)] =
Therefore:
δ = θ - A +
arcsin[n sin (A - arcsin (sin θ)/n)]
(1)
The minimum deviation δm is determined as follows:
dδ/d θ = 0
We know that d[arcsin x ]/dx = 1/(1 - x2)1/2
If f(x) = arcsin (x) then sin f(x) = x; and by a derivative :
f'(x) cos f(x) = dx/dx = 1, therefore: f'(x) = 1/[1 - sin2f(x)]1/2 =
1/[1 - x2]1/2
Then:
dδ/d θ = 1 + 1/[1 - (arcsin[n sin (A - arcsin (sin θ)/n)] )2]1/2
x n cos(A - arcsin (sin θ)/n) x {- 1/sqrt[1 - (sin θ)/n]2)1/2} x (cosθ)/n) =
dδ/d θ = 0 leads to:
1 = 1/[1 - (arcsin[n sin (A - arcsin (sin θ)/n)] )2]1/2
x cos(A - arcsin (sin θ)/n) x {1/sqrt[1 - (sin θ)/n]2)1/2} x cosθ)
This equation is satisfied by the relationship:
sin θ = n sin (A/2)
(2)
2. Minimal deviation for a prism:
We have then the expression of the minimum angle of deviation :
δm = 2 θ - A
(3)
The equation (2) becomes:
sin[(δm + A)/2] = n sin (A/2)
(4)
The first five relationships along with the relationship (2) give:
sin θ = n sin r1
→ r1= A/2, and i = A/2. Then i = r1
n sin i = sin r2 → n sin (A/2) = sin r2 →
r2 = θ
The angle:
π/2 - θ + a = π/2 - r1 = π/2 - A/2. It forms then
with the bisect of angle A a right angle. Therefore, the refracted ray within
the medium n is perpendicular to the bisect of angle A (then horizontal).
|
|