Optics: Refraction of light
The second law of Geometrical Optics:
Refraction of light:
When light is incident at an interface between two media, it is partly reflected
and partly transmitted. The transmitted ray is called the refracted ray.
1. Index of refraction:
The index of refraction "n" for a medium (transparent optical medium) is defined as the
ratio of the speed of light in a vacuum "c" to the speed of light in the medium "v".
n = c/v
Example of index of refraction:
Vacuum: 1
Air: 1.0003
Water: 1.33
Diamond: 2.42
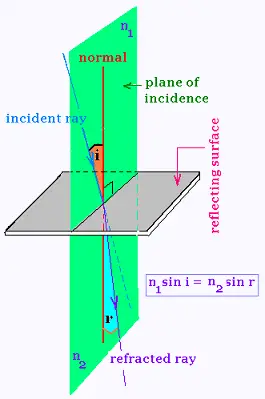
2. Snell's law:
The refracted ray bends toward the normal to form an angle
less than the angle of incidence if the refraction index of the refracting medium is
grater than the one of the incidence medium
.
According to n1 sin i = n2 sin r, if n2 > n1, then i > r; the ray bends then
toward the normal. And if if n2 < n1, then i < r and he ray bends then
backward the normal.
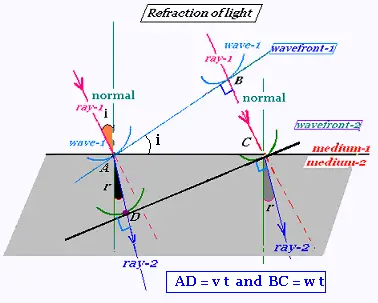
We have:
t = AD/v = BC/w
sin r = cos DAC = AD/AC
We have shown that BAC = i. Then:
sin i = BC/AC
Therefore:
AC = AD/sin r = BC/sin i → AD sin i = BC sin r → v sin i = w sin r.
The index of refraction of the first medium is c/w = n1; and the index
of refraction of the second medium is c/v = n2.
The relation
v sin i = w sin r becomes: n1 sin i = n2 sin r.
n1 sin i = n2 sin r
This is Snell's law.

|