Physique 23 : Optique géométrique

Dioptres sphériques

1. Définition

Un dioptre est l'ensemble de deux milieux homogènes d'indices de réfraction différents n1 et n2 séparés par une surface. Si cette surface est sphérique, le dioptre est sphérique. Si la surface est plane, le dioptre est plan.

2. Formule de conjugaison des dioptres
origine au sommet S du dioptre:

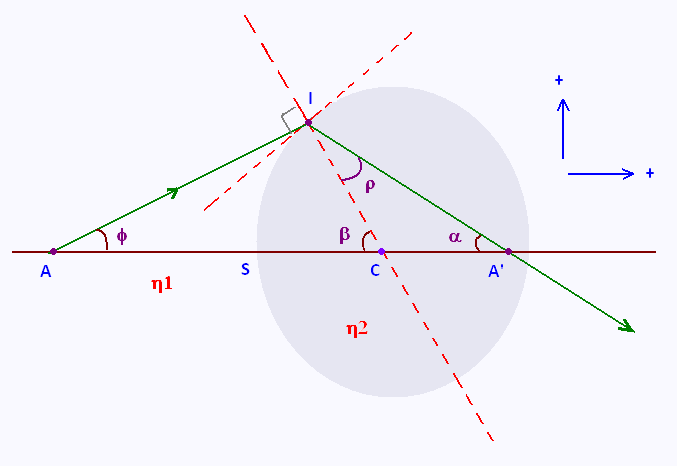
Dans l'approximation de Gauss, ces angles sont petits, on confond alors les sinus et les angles en radians:

φ + β = i
β = ρ + α

La loi de Snell s'ecrit:

n₁ (φ + β) = n₂(β - α)

Il vient:

(n₂ - n₁) β = n₁ φ + n₂ α      (1)

Nous avons:

φ = $\large\bf{ \frac{SI}{\overline{AS}} }$

β = $\large\bf{ \frac{SI}{\overline{SC}} }$

α = $\large\bf{ \frac{SI}{\overline{SA'}} }$

La relation (1) devient:

$\bf\Large\color{green}{ \frac{n_2} {\overline{SA'}} - \frac{n_1} {\overline{SA}} = \frac{n_2 - n_1} {\overline{SC}} }$      (2)

3. Formule de conjugaison des dioptres
origine au centre C du dioptre:

Partons de :

$\large\bf{ \frac{n_2}{\overline{SA'}} - \frac{n_1}{\overline{SA}} = \frac{n_2 - n_1}{\overline{SC}} }$

Nous avons:

$\bf{ \overline{SA'} = \overline{SC} + \overline{CA'} \\ \overline{SA} = \overline{SC} + \overline{CA} \\ \overline{SC} = - \overline{CS} }$

Donc:

$\large\bf{ \frac{n_2}{\overline{SC} + \overline{CA'} } - \frac{n_1}{\overline{SC} + \overline{CA} } = - \frac{n_2 - n_1}{\overline{CS}} }$

Le produit des extrêmes est égal au produit des moyens donne:

$\bf{ \frac{ n_2\overline{SC } + n_2\overline{CA } - n_1 \overline{SC } - n1 \overline{ CA'} } { ( \overline{SC }+ \overline{CA' })(\overline{SC } + \overline{CA}) } = - \frac{n_2 - n_1}{\overline{CS}} }$

On développe et on simplifie:

$\bf{ - \overline{CS} ( (n_2 - n_1)\overline{SC} + n_2 \overline{CA} - n_1\overline{CA'} ) = \\ (n_2 - n_1)( \overline{SC} + \overline{CA' })(\overline{SC } + \overline{CA}) \\ \text{ } \\ n_1 \overline{CA'} \; . \; \overline{CA} - n_2 \overline{CA'} \; . \; \overline{CA} = \\ n_2 \overline{CA'} \; . \;\overline{SC} - n_1\overline{CA} \; . \;\overline{SC} \\ \text{ } \\ (n_1 - n_2)\overline{CA'} \; . \;\overline{CA} = \\ n_1\overline{CA} \; . \;\overline{CS} - n_2 \overline{CA'}\overline{CS} }$

On divise par le produit: $\overline{CA} \times \overline{CA'}$

On obtient:

$\bf\Large\color{green}{{ \frac{n_1}{\overline{CA'}} - \frac{n_2}{\overline{CA}} = \frac{n_1 - n_2}{\overline{CS}} } }$

2. Formule de conjugaison des dioptres
Résumé

Dans l'approximation de Gauss, nous avons:

1. Origine au sommet S:

$$\bf\large\color{blue}{ \frac{n_2}{\overline{SA'}} - \frac{n_1}{\overline{SA}} = \frac{n_2 - n_1}{ \overline{SC}} }$$

2. Origine au centre C:

$$\bf\large\color{indigo}{ \frac{n_1}{\overline{CA'}} - \frac{n_2}{\overline{CA}} = \frac{n_1 - n_2}{ \overline{CS}} }$$

3. Origine aux foyers:

$$\bf\large\color{brown}{ \overline{F'A'} \times \overline{FA} = \overline{SF'} \times \overline{SF} }$$