Optique 4
Exercices
Optique 32
Exercices
Optique Gécep
© The scientific sentence. 2010
|
Physique 23 : Optique géométrique
Dioptres sphériques et lentilles
exercices divers
Exercice 1 : Lentille demi-boule
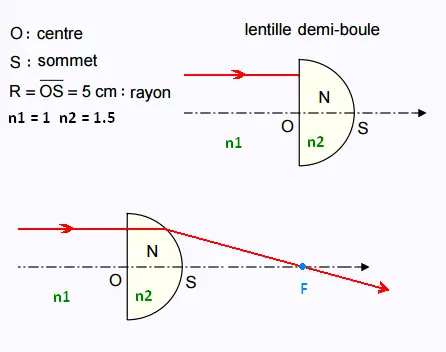
Considère une lentille demi-boule de centre O, de sommet S,
de rayon R = OS = 5 cm = et d'indice
n2 = 1,5 , dans l'air d'indice n = 1.
1. Dans l'approximation de Gauss, déterminer la position
du foyer image F de cette lentille.
2. La lentille est éclairée par des rayons parallèles à l'axe
optique OS, à la distance R/2 de cet axe.
En réalité, l'image ne se forme pas sur le foyey image F. Elle
se forme à un point G proche de F.
Déterminer alors l'aberration de sphéricité FG.
1. Dans l'approximation de Gauss, la relation de conjugaison d'un dioptre sphérique avec origine au centre O s'écrit :
n2/OA' - n1/OA = (n2 - n1)/OC
OC = OS = R
n2/OA' - n1/OA = (n2 - n1)/R
L'objet st à l'infini, donc OA = ∞ .
D'où:
n2/OA' = (n2 - n1)/R
OA' = n2 R /(n2 - n1)
L'objet st à l'infini, donc son image se
forme sur le foyer image F
D'où:
OF = n2 R /(n2 - n1)
OF = 1.5 x 5 /(1.5 - 1) = 15 cm.
OF = 15 cm.
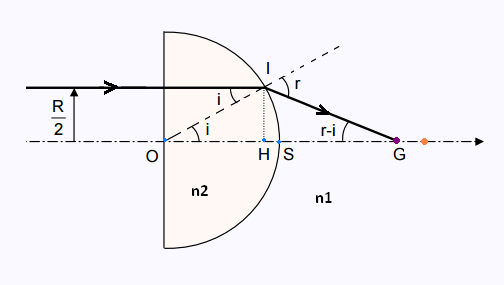
2. Dans le triangle OHI :
tan i = IH/OH
OH = IH/tan i
Dans le triangle GIH :
tan(r - i) = IH/HG
HG = IH/tan(r - i)
Or OG = OH + HG = IH/tan i + IH/tan(r - i)
IH [1/tan i + 1/tan(r - i)]
OG = (R/2) [1/tan i + 1/tan(r - i)]
sin i = (R/2)/R = 1/2. D'où I = 30o
La loi de Snell-Descartes s'ecrit:
n2 sin i = n1 sin r . D'où:
sin r = (n2/n1) sin i
sin r = (1.5 /1) sin 30 = 1.5 x 1/2 =
3/4 = 0.75.
r = sin- 1 (0.75) = 48.6o
OG = (5/2) [1/tan(30) + 1/tan(18.6)] = 11.76
OG = 11.76 cm
GF = OF - OG = 15 - 11.76 = 3.24 cm
GF = 3.24 cm
Exercice 2 : Lentille boule
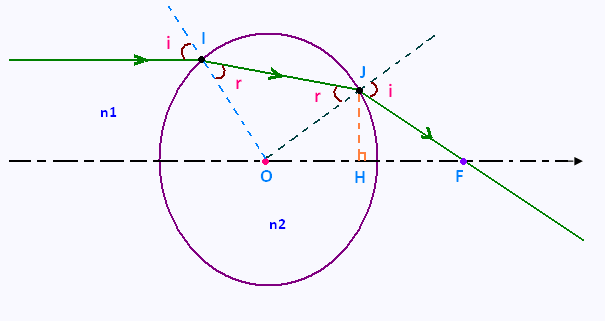
On considère une lentille sous forme de boule en verre de rayon R et d’indice n2, dans l'air d'indice égale à n1 = 1.
On veut montrer dans l’approximation de Gauss qu’elle est équivalente à une lentille mince.
1. Déterminer la relation de conjugaison de cette lentille boule et en déduire sa distance focale image f en fonction de R et de n2.
2. Donner l’expression du grandissement γ de cette lentille.
1. L'image A" de A par le premier dioptre sphérique de sommet S est donnée par la relation de
conjugaison suivante avec origine au centre O :
n1/OA" - n2/OA = (n1 - n2)/OS
L'image A' de A" par le second dioptre sphérique de sommet S est donnée par la relation de
conjugaison suivante avec origine au centre O :
n2/OA' - n1/OA" = (n2 - n1)/OS
En fontion de R, on a:
n1/OA" - n2/OA = (n1 - n2)/(- R)
n2/OA' - n1/OA" = (n2 - n1)/(+ R)
Additionnant memebre à membre, il vient;
n2/OA' - n2/OA = 2 (n2 - n1)/R
1/OA' - 1/OA = 2 (n2 - n1)/n2R
On peut ecrire aussi:
1/OA' - 1/OA = 1 /(n2R /2(n2 - n1))
C'est la relation de conjugaison d'une
lentille mince de la longueur focale:
ƒ = n2 R /2(n2 - n1)
2. Le grandissement du premier dioptre est:
Le grandissement du second dioptre est:
Le grandissement du système de la lentille boule est:
Le système de la lentille boule est équivalent à une lentille mince
de longueur focale ƒ = n2 R /2(n2 - n1), et
d'agrandissement γ = γ1 x γ2, produit des agrandissements des deux dioptres.
|
|