Physique 23 : Optique

Lentilles minces
Lentilles convergents
Lentilles divergents

Exercice 1 : Position d'un objet
sur l'axe optique d'une lentille

Un objet est observé à travers une lentille de vergence – 5 δ.

a) Montrer que cette lentille donne d'un objet réel une image virtuelle.
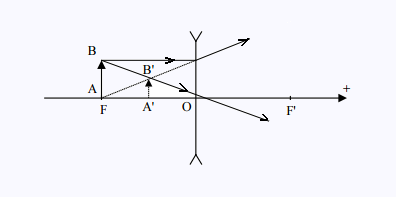
b) Construire l'image A'B' de l'objet AB.
c) Où situer l'objet pour que l'image qu'elle en donne ait le grandissement 0.25 ?
d) Où situer l'objet pour que l'image qu'elle en donne ait le grandissement 0.50 ?

a) Vergence C = – 6 δ donc ƒ = 1/C = 1/(- 5) = - 1/5 = - 0.2 m = - 20 cm.

$$\large\bf\color{brown}{ \overline{OF} = - 20 \; cm. }$$
La distance focale est négative, la lentille est donc divergente. Elle donne ainsi d'un objet réel une image virtuelle.


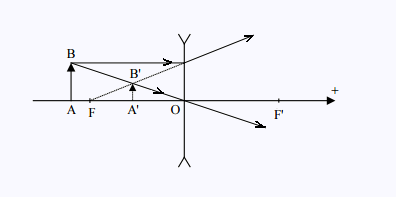
Nous avons:

$\large\bf\color{brown}{ \gamma = \frac{A'B'}{ \overline{AB}} = \frac{OA'}{ \overline{OA}} }$

On applique la formule:

$\bf\color{indigo}{ \frac{1}{ \overline{OA'}} - \frac{1}{ \overline{OA}} = \frac{1}{ \overline{OF}} \\ \frac{1}{\gamma \overline{OA}} - \frac{1}{ \overline{OA}} = \frac{1}{ \overline{OF}} \\ \frac{1}{\overline{OA}} (\frac{1}{\gamma} - 1) = \frac{1}{ \overline{OF}} \\ \overline{OA} = \overline{OF} (\frac{1}{\gamma} - 1) \\ \text{ } \\ \text{ c) } \; \overline{OA} = - 20 \times (\frac{1}{0.25} - 1) \\ = - 20 \times (4 - 1) = - 60 cm = - 0.60 m \\ \text{ 60 mètres à gauche de la lentille} \\ \text{ } \\ \overline{OA} = - 20 \times (\frac{1}{0.50} - 1) = \\ - 20 \times (2 - 1) = - 20 cm = - 0.20 m \\ \text{ } \\ \text{ d) 20 mètres à gauche de la lentille,} \\ \\ \text{ c'est à dire sur le foyer principal.} }$

Exercice 2 Lumière à travers une vitre

Une lumière traverse une vitre.

a) Montrer que la lumière n’est pas déviée lors de son passage à travers une vitre.

b) Quelle est la valeur du décalage latéral maximal ?

c) Quel sera le trajet de la lumière si la vitre n’a pas ses faces rigoureusement parallèles ?



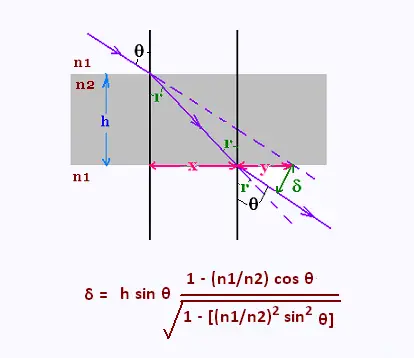
La loi de la réfraction donne :

• À l'entrée de la vitre:

n_air sin θ = n_vitre sin r

• À la sortie de la vitre:

n_vitre sin r' = n_air sin θ’

Les faces de la vitre sont parallèles, les angles alternes internes r et r' sont alors isométriques. r = r'.

r est l'angle de réfraction dans la vitre et r' est l'angle d'incidence dans l'air en sortant de la vitre.

Il vient donc:

θ = θ'

C'est à dire que la lumière n'est pas déviée.

b) La déviation δ est donnée par la formule ( voir démonstration ):

δ = h sin θ [1 - (n1/n2) cos θ/ (1 - [(n1/n2)² sin² θ])^1/2]

Cette valeur est maximale lorsque θ = 90^o.

c) Si la vitre n’a pas ses faces rigoureusement parallèles r sera different de r' et θ sera différent de θ'. La lumière sera donc est déviée.