Physique 23 : Optique
Miroirs sphériques
Equation fondamentale des miroirs
Origine en S
1. Equation fondamentale des miroirs
avec l'origine au centre S du miroir
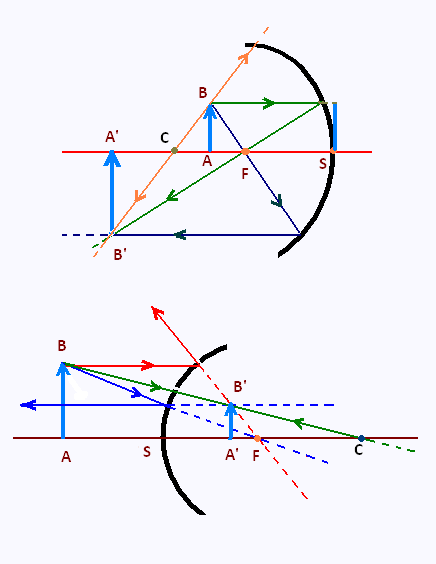
Nous avons établi la relation
fondamentale des miroirs sphériques:
1/CA' - 1/CA = 1/ƒ
C est le centre de courbure du miroir,
A' est l'image du point A sur l'axe optique, et
ƒ est la longeur focale du miroir.
CA, CA' et CS = ƒ sont les longeurs des segments
correspondants.
Nous allons redéfinir cette formule en fonction, plutôt,
du sommet S du miroir, concave ou convexe.
Nous avons:
CA/CA' = AB/A'B' = SF/FA'
De plus:
CA' = SA' - CS
CA = CS - SA
FA' = SA' - SF
Le rapport:
CA'/CA = FA'/SF
devient:
(SA' - CS)/(CS - SA) = (SA' - SF)/SF
Le produit des extrêmes est égal au produit des moyens
s'ecrit:
SF(SA' - CS) = (SA' - SF)(CS - SA)
On factorise:
SA' SF - CS SF = SA'CS - SA SA' - SF CS + SF SA
On réduit:
SA' SF = SA'CS - SA SA' + SF SA
Or CS = 2 SF. Donc
SA' SF = 2 SF SA' - SA SA' + SF SA
SA SA' - SF SA = SF SA'
On factorise, puis on divise les deux membres de
l'équation par le produit SA SA' :
(SA SA' - SF SA)/SA SA' = SF SA' /SA SA'
On obtient:
1 = SF/SA + SF/SA' , ou
1/SA + 1/SA' = 1/SF
1/SA + 1/SA' = 1/SF = 1/ƒ
1/SA + 1/SA' = 1/SF = 1/ƒ
Telle est la relation fondamentale des miroirs sphériques
avec origine au centre S du miroir. Cette formule est dite aussi
relation de Descartes .
SA et SA' sont les distances entre le centre du miroir S et
le point A et son image A' respectivement.
2. Grandissement
Le grandissement est le nombre algébrique, rapport entre les dimensions de l'image et de l'objet:
|