La propagation de la lumière
Réflexion et réfraction de la lumière
La lumière
Les lois de la réfraction
Indice de réfraction et dispersion
Spectres et lumières
Spectres d'émission et spectres d'absorption

1. La propagation de la lumière
Ondes et applications médicales

1.1. La lumière

La lumière est une onde électromagnétique visible. Elle est donc caractérisée par une fréquence comprise entre 3.5 x 10¹⁴ Hz et 7.5 x 10¹⁴ Hz. Elle correspond à la propagation du champs électriques et magnétique dans le vide et certains milieux matériels.

1.2. La trajectoire de la lumière

Dans le vide, la lumière se propage de manière rectiligne (en suivant une droite). Son trajet est donc représenté par un rayon lumineux (une droite comportant une flêche).

Dans un milieu matériel, seul certains les matériaux transparents laissent la lumière se propager. Dans un milieu transparent la propagation de la lumière n'est alors rectiligne que si ce dernier est homogéne.

1.3. La vitesse de la lumière dans le vide

La vitesse de la lumière dans le vide est égale à c = 300 000 km/s

1.4. La vitesse de la lumière dans un
milieu matériel transparent

Dans un milieu transparent la lumière se propager moins vite que dans le vide. La vitesse de propagation s'epxrime alors à l'aide de la relation suivante: v = c/n

où v est la vitesse de la lumière dans le milieu transparent (en mètre par seconde) ,
c est la célérité de la lumière dans le vide. c = 300 000 000 m/s .

n est l'indice de réfraction. Il est sans unité.

L'indice de réfraction est caractéristique de chaque type de milieu transparent. n est toujours supérieur ou égale à 1.

Dans l'air n = 1 ce qui signifie que la vitesse de propagation est la même que dans le vide.

Par contre dans l'eau n = 1.3 et dans le verre n = 1.5 donc dans ces milieux, la lumière se propage moins vite que dans le vide.

2. Réflexion et reflexion de la lumière
Santé - Ondes et applications médicales

2.1. La réfraction de la lumière

lorsque la lumière atteint un nouveau milieu une partie de cette dernière s'y propage mais en subissant une déviation. Ce phènomène correspond à une réfraction.

Réfraction d'un rayon lumineux passant d'un milieu 1 d'indice de réfraction n1 à un milieu 2 d'indice de réfraction n2.

Voici les termes utilsées:

• Rayon incident: il s'agit du rayon de lumière se propageant dans le premier milieu.
• Rayon réfracté: il s'agit du rayon de lumière se propageant dans le deuxième milieu et qui a donc subit une réfraction .
• Normale: c'est la droite perpendiculaire à la surface de séparation des deux milieux.
• Angle d'incidence i: angle entre le rayon incident et la normale.
• Angle de réfraction r: angle entre le rayon réfracté et la normale.

Lors de la refraction d'un rayon de lumière, la déviation subit par le rayon lumineux en changeant de milieu dépend de la différence d'indice de réfraction entre les deux milieux:

• Si n1 < n2, on dit que le milieu 2 est plus réfringent que le milieu 1. Le rayon réfracté se rapproche de la normale.

• Si n1 > n2, le milieu 1 est plus réfringent que le milieu 2. Le rayon réfracté s'éloigne de la normale.

2.2. La réflexion de la lumière

Lorsque la lumière atteint un nouveau milieu une partie est réfractée tandis que l'autre partie est renvoyée dans le premier milieu: on dit que cette lumière est réfléchi ou subit une réflexion.

2.3. La réflexion totale de la lumière

Dans le cas ou la lumière passe dans un milieu moins réfringent, elle s'éloigne la normale. Au delà d'une certaine limite de l'angle d'incidence, la réfraction n'est alors plus possible et la lumière est entièrement réflechie. C'est la reflexion totale.

Ce phénomène de reflexion totale fait du diamant la pière la plus brillante.

Le phénomène est en particulier mis à profit dans les fibres optiques et fibroscopie, où la lumière entre avec un angle d'incidence trop important pour ne subir aucune réfraction et se réfléchir entièrement.

3. L'univers: Réflection et réfraction de la lumière
Les lois de la réfraction

3.1. La réfraction

Lorsque la lumière passe d'un milieu transparent à un autre elle subit une déviation. C'est cette déviation qui correspond au phénomène de réfraction. La réfraction est décrites par les lois de Snell-Descartes.

• Première loi de Snell-Descartes:

Cette loi indique que le rayon lumineu réfracté, appartient au même plan que la normale et le rayon incident.

• Deuxième loi de Snell-Descartes:

Cette loi permet de déterminer l'angle de réfraction: Si un rayon lumineux passe d'un milieu d'indice de réfraction n1 à un milieu d'indice de réfraction n2 alors il existe la relation suivante entre l'angle d'incidence i et l'angle de réfraction r:

n1 sin (i) = n2 sin (r)

• Prévoir le sens de déviation d'un rayon réfracté:

D'après la deuxième loi de Snell-Descartes:

- Si le premier milieu est plus réfringent que le deuxieme, c'est à dire si n1 > n2 cela signifie que le rapport des indices est supérieur à 1 et donc r > i : le rayon réfracté s'éloigne de la normale.

- Si le deuxième milieu est plus réfringent que le premier, c'est à dire si n2 > n1 cela signifie que le rapport des indices est inférieur à 1 et donc r < i: le rayon réfracté se rapproche de la normale.

• Calculer l'angle de réfraction:

L'utilisation de la deuxième loi de Snell-Descartes permet d'obtenir la relation : sin (r) = (n1/n2) sin (i)

Lorsque la valeur de sin (r) est connue il suffit d'utiliser, sur une calculatrice, la fonction inverse du sinus ( souvent notée sin-1). Selon les paramètre utilisé la calculatrice indique l'angle de réfraction en degré ou en radian.

4. Indice de réfraction et dispersion de la lumière

4.1. Indice de réfraction

On peut déterminer expérimentalement un indice de réfraction ;

Pour déterminer l'indice de réfraction d'un milieu il suffit d'effectuer la réfraction d'un rayon lumineux puis de mesurer les angles d'incidence (i) et de réfraction (r). L'utilisation de la deuxième loi de Snell-Descartes permet d'obtenir la relation:

n2 = n1 sin (i)/ sin(r)

Par ailleur si le premier est l'air alor n1 = 1 donc la relation devient: n2 = sin (i)/sin(r)

• Définition de l'indice de réfraction

L'indice de réfraction (n) d'un milieu est definit comme le rapport de la vitesse de la lumière dans le vide (c) par la vitesse de la lumière dans ce milieu ( v ):

n = c/v

où c et v sont exprimées avec les même unité de vitesse mètre par seconde ou kilomètre par seconde en général )

• L'indice de réfraction étant défini comme le rapport de deux grandeurs de même unité , il ne possède donc pas d'unité.

• Dans un milieu matériel la vitesse de la lumière ne peut être supérieure à celle possédée dans le vide. Ainsi, un indice de réfraction est toujours supérieur ou égal à 1.

• Indice de réfraction de quelques milieux:

L'indice de réfraction est une caractéristique d'un milieu, c'est donc une grandeur physique que peut être utilisée pour identifier une substance.

Indice de réfréaction des milieux les plus courant:

Milieu Air eau verre Rubi Diamant

indice 1,00 1,3 1,5 1,8 2,5

L'indice de réfraction d'un milieu dépend de sa température. Il diminue avec la témpérature.

• Calculer la vitesse de la lumière dans un milieu:

L'expression de l'indice de réfraction d'un milieu permet de déterminer la vitesse de la lumière dans ce milieu:

v = c/n

Par exemple dans le verre: v = 300 000/1.5 = 200 000 km.s-1 .

4.2. La dispersion

L'indice de réfraction d'un milieu dépend de la longueur d'onde de la lumière qui le traverse: l'indice est légèrement plus faible pour les lumières de longueur d'onde élevée.

Une des conséquences de ce phénomène est qu'il se produit une réfraction différente pour des lumières de longueurs d'onde différentes.

Ainsi une lumière violette est plus réfractée qu'une lumière rouge. Les différentes lumières composant une lumière polychromatique sont ainsi refractées dans des directions légèrement différentes.: il y a dispersion de la lumière.

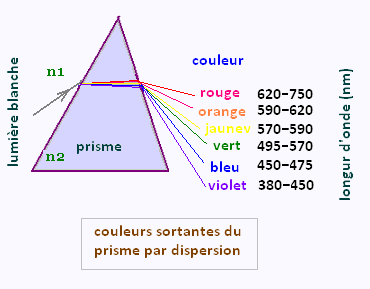
Ce phénomène peut être accentué et nettement observer lorsque la lumière traverse un prisme. Il se produit aussi naturellement lorsque les gouttes de pluies réfractent la lumière du Soleil et forment un arc-en-ciel.

5.L'univers: Analyse de la lumière des étoiles

5.1. Lumière et longueur d'onde

La lumière est constituée de rayonnements électromagnétiques qui se distinguent par leur fréquence. On utilise cependant une autre grandeur pour caractériser chaque rayonnement: la longueur d'onde. Elle est symbolisée par la lettre grecque λ (lambda) et s'exprime en unités de longueur, généralement le nanomètre.

La longueur d'onde d'une lumière visible se trouve entre 400 nanomètres (pour le violet) et 800 nanomètres pour le rouge.

5.2. Lumières monochromatiques et
polychromatiques

On distingues les lumières monochromatiques qui sont caractérisées par un rayonnement de longueur d'onde unique et les lumières polychromatiques qui comportent des rayonnements caractérisés par plusieurs longueurs d'onde.

La lumière du soleil est une lumière blanche. C'est un exemple de lumière polychromatiqu. La lumière produite par un laser est monochromatique.

5.3. Les spectres

Un spectre correspond à l'ensemble des rayonnements qui constituent une lumière. L'étude et l'obtention des spectres s'appelle la spectroscopie. Elle permet d'obtenir des informations sur la nature de la matière qui produit cette lumière ainsi que sur les milieux qu'elle a traversée.

L'analyse de du spectre d'une étoile permet ainsi de déterminer sa température ainsi que la composition de son atmosphère.

6. Les spectres d'émission et d'absorption

6.1. Les spectres d'émission:

Les spectres d'émission sont constitués des rayonnements émis par un corps. On distingue deux sortes de spectre d'émission:

1. Les spectres continus: ils sont d'origine thermique et l'émission de lumière produite est liée à la température de la source. Ce type de spectre comporte tous les rayonnements visibles sans discontinuité du violet au rouge.

Cependant la proportion des différents rayonnements n'est en général pas la même et un spectre d'émission continu comporte toujours une longueur d'onde correpondant à une intensité plus forte que les autres.

Cette longueur d'onde qui correspond à un maximum d'émission permet de déduire la température du corps émetteur. Plus cette longueur d'onde est faible (décalé vers le violet ) et plus la température est élevée.

Les spectres continus permettent donc de déterminer la température de leur source. C'est ainsi que la température de surface d'une étoile peut être connue.

2. Les spectres de raie: ils sont constitués uniquement de quelques raies correspondant à un nombre limité de longeurs d'onde. Ils sont obtenus par excitation électrique de certains gaz.

Chaque composé chimique possède son propre spectre de raie qui le caractérise et permet de l'identifier.

6.2. Les spectres d'absoption :

Un spectre d'absorption est obtenu lorsque qu'une lumière blanche ayant un spectre continue traverse une substance. Sur cette substance, certains rayonnements provoque l'apparition de raies noires sur le spectre initialement continu.

Les longueurs d'ondes absorbées par une substance correspondent aussi aux longueurs d'ondes des rayonnement figurant dans son spectre de raie d'émission.

Les raies noires figurant dans un spectre d'absorption permettent donc d'identifier les substances qui ont été traversées par la lumière.

L'analyse d'un spectre de raie permet d'identifier les substances présentes dans l'atomsphère d'une étoile.