Optique 4
Exercices
Optique 32
Exercices
Optique Gécep
© The scientific sentence. 2010
|
Physique 23 : Optique géométrique
Prismes
Exercice 1 : Prisme isocèle rectangle.
On considère un prisme isocèle rectangle.
Le rayon incident rentre perpendiculairement à un
côté de l'angle droit se refléchi totalement su l'hypoténuse
et sort perpendiculairement à l'autre côté de
l'angle droit.
a) Montrer que l'angle i mesure 45o.
b) A quelle relation doit satisfaire l'indice n du prisme
pour que l’on se trouve dans le cas d’une réflexion totale ?
c) Comment se comporte alors le prisme ?
d) Quel sera la position du prisme pour qu'il renvoye
la lumière en sens inverse.
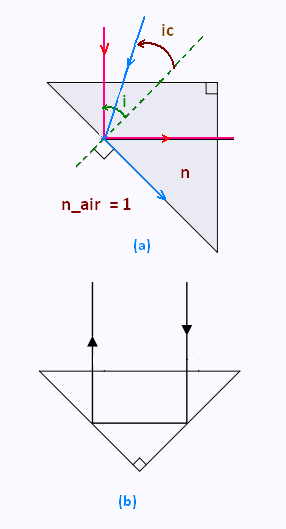
a) Les angles à la base d'un triangle isocèle rectangle
valent 45o chacun.
Donc la normale fait un angle de 45o avec
le côté horizontal du triangle isocèle rectangle.
Cet angle est le complémentaitre de l'angle i. Ainsi
i mesure 45o .
b) Pour qu’il y ait réflexion totale il faut deux conditions :
n > n_air et i > ic ( angle critique) .
La fonction sinus est croissante dans [0, π/2] , don
sin i > sin ic
Nous avons : sin ic = n_air/n
( voir démonstration ):
sin i > n_air/n
n > n_air/sin i = 1/sin 45 1/(√2 /2) = √2 = 1.41.
n > 1.41.
c) Le prisme se comporte comme un miroir.
d) Une rotation du prisme de 45 + 90 = 135o
dans le sens horaire donne la position ou la lumière
est renvoyée dans le sens inverse (figure b).
Exercice 2 : Prisme et plusieurs reflexions
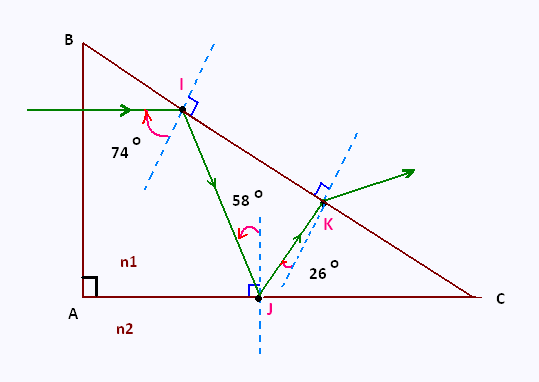
On considère un prisme de verre ABC d'indice n1,
rectangle en A, plongé dans un milieu d'indice n2.
L'angle B mesure 74o.
Un rayon lumineux rencontre le prisme
perpendiculairement à AB, puis fait des réflexions en I, J
et une réfraction en K.
On considère deux milieux
qui entoure le prisme. Le premier est l'air, d'indice
n2 = n_air = 1, le deuxième d'indice n2 à déterminer
pour que le rayon subisse toujours deux refléxions totales,
une en I, et l'autre en J.
1) n1 = 1.5, et n2 = 1
En I, J et K l'angle critique est tel que:
n1 sin ic = n2. Donc:
ic = sin- 1(n2/n1)
= sin- 1(1/1.50) = 42o
ic = 42o
En I, l'angle d'incidence 74o > ic;
il y a donc réflexion totale.
En J, l'angle d'incidence 58o > ic;
il y a donc réflexion totale.
En K, l'angle d'incidence 26o < ic;
il ya donc réflexion partielle.
2) n1 = 1.5 et n2 = ?
• En I, pour avoir une réflexion totale,
l'angle d'incidence i doit satisfaire l'inégalité:
i > ic . Donc:
n1 sin i > n1 sin ic = n2 , soit
n1 sin i > n2
n2 < n1 sin i
n2 < 1.50 sin 74 = 1.442
n2 < 1.442
• En J, pour avoir une refléxion totale,
l'angle d'incidence i doit satisfaire de nouveau
l'inégalité:
i > ic . Donc:
n2 < 1.50 sin 58 = 1.272
n2 < 1.272
• En K, pour avoir une refléxion partielle,
l'angle d'incidence i doit satisfaire l'inégalité:
i < ic
n1 sin i < n1 sin ic = n2
n1 sin i1 < n2
n2 > n1 sin i1
n2 > 1.50 sin 26 = 0.658
n2 > 0.658
On a donc 3 inégalités:
En I: n2 < 1.442
En J: n2 < 1.272
En K: n2 > 0.658
Qu se réduisent à deux égalités:
n2 < 1.272
n2 > 0.658
En tout
0.658 < n2 < 1.272
|
|