Physique 23 : Optique
Miroirs
Equation fondamentale des miroirs
1. Equation fondamentale des miroirs
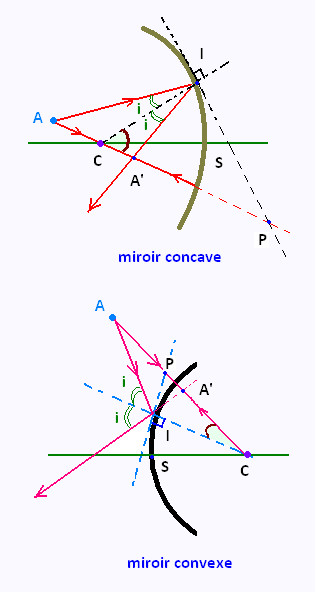
Soit un miroir sphérique, concave ou convexe, de centre de courbure C et de sommet S et A un point lumineux.
Considérons un rayon incident issu du point A et refléchissant en I. A' est l'image de A.
Pour le miroir concave, IC est la bissectrice de l'angle AIA'.
Pour le miroir convexe, IP est bissectrice de l'angle AIA'.
Dans le triangle CIA, on a la relation:
CA/sin i = CI/sin A
Dans le triangle CIA', on a la relation:
CA'/sin i = CI/sin (π - 2i - A)
D'où
CA/CA' = (CI sin i/sin A ) x (sin (π - 2i - A) / CI sin i ) =
sin (π - 2i - A)/sin A = sin (2i + A)/sin A
CA/CA' = sin (2i + A)/sin A (1)
Dans le triangle API, nous avons:
PA/sin(π/2 + i) = IP/sin A
PA = IP cos i/sin A
Dans le triangle A'PI, nous avons:
PA'/sin(π/2 - i) = IP/sin A'
PA'= IP cos i/sin (π - 2i - A) =
IP cos i/sin (2i + A)
PA/PA' = sin (2i + A)/ sin A (2)
En comparant les relations (1) et (2), on
obtient:
CA/CA' = PA/PA' = sin (2i + A)/sin A
PA/PA' = (PC + CA)/ (CP - CA')
CA/CA' + 1 = (PC + CA)/ (CP - CA') + 1
(CA + CA')/CA' = [(PC + CA) + (CP - CA') ]/(CP - CA')
= (2PC + CA - CA') /(CP - CA')
(CP - CA')(CA + CA')/CA' = 2PC + CA - CA'
CP CA + CP CA' - CA' CA - CA' CA' = 2PC CA' + CA CA' - CA'CA'
CP CA = PC CA' + 2 CA CA'
CA = CA' + 2 CA CA'/CP = CA'(1 + 2 CA /CP)
CA/CA' = 1 + 2 CA /CP
1/CA' = 1/CA + 2/CP
1/CA' - 1/CA = 2/CP
Or CI = CS = R : rayon de courbure du miroir. Donc,
avec α = ∠ICA' = , on a:
R = CP cos α ou
CP = R/cos α . Donc:
1/CA' - 1/CA = 2 cos α /R
1/CA' - 1/CA = 2 cos α /R
Telle est l'équation fondamentale des miroirs
sphériques.
2. Equation fondamentale des miroirs
dans les conditions de gauss
Dans les conditions de gauss, l'angle α est
faible, cos α = 1 et on retrouve
la formule pour les rayons paraxiaux:
1/CA' - 1/CA = 2/R
En posant R/2 = ƒ ou ƒ est le longueur
focale du miroir, on obtient:
1/CA' - 1/CA = 1/ ƒ
1/CA' - 1/CA = 1/CS = 2/R = 1/ƒ
3. Cas particliers
3.1. Le point lumineux est situé
sur l'axe optique
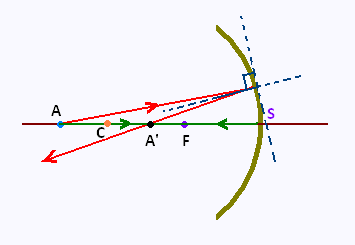
Le point lumineux A est situé sur l'axe optique.
Son image A' est aussi sur l'axe optique.
N'importe quel rayon incident issu du point A est refléchi par le miroir selon la deuxième loi de
reflection.
Le rayon refléchi coupe l'axe optique
en A' qui est l'image du point A.
Pour trouver la position de A', on applique la relation
fondamentale des miroirs sphériques:
1/CA' - 1/CA = 1/ƒ
3.2. Construction de l'image
d'un objet
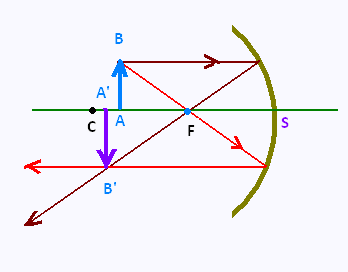
Le corps lumineux est un objet constitué de plusieurs points.
Les tracés des rayons d'un point quelconque et d'un
point sur l'axe optique permettent la construction
de l'image d'un objet.
Pour trouver la position de A', on applique la relation
fondamentale des miroirs sphériques:
1/CA' - 1/CA = 1/ƒ
3.3. Image d'un objet entre le
foyer et le centre d'un miroir courbe
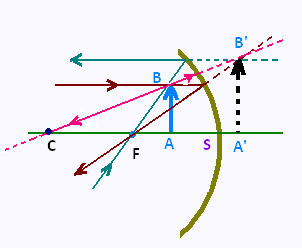
Les tracés des rayons principaux permettent la construction de l'image d'un objet.
Noua avons CA' > CA . Si donc on applique la relation
fondamentale des miroirs sphériques:
1/CA' - 1/CA = 1/ƒ
On trouve que le premier membre de la relation
est négatif. Le second membre de cette formule ne
contient que la distance focale positive. La solution
c'est de refaire la géométrie
de la situation.
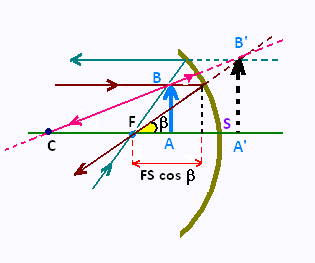
AB//A'B'. D'après le théorème de Thalès:
CA/CA' = AB/A'B' = FS cos β/FA'
Nous avons:
FA' = CA' - CF
CF = FS
Donc:
CA/CA' = FS cos β/(CA' - FS)
Le produit des extrêmes est égal au produit des moyens
donne:
CA (CA' - FS) = CA' FS cos β
On développe:
CA CA' - CA FS = CA' FS cos β =
CA FS + CA' FS cos β = FS(CA + CA' cos β)
On réduit:
FS(CA + CA' cos β) = CA CA'
On divise les deux membres de la formule par
le produit CA CA':
1/CA + cos β/CA' = 1/FS
On obtient;
cos β/CA' + 1/CA = 1/FS
Lorsque β ≈ 0 , C'est à dire dans les
conditions de Gauss, on retrouve alors
la relation fondamentale des miroirs sphériques,
à un signe près.
1/CA' + 1/CA = 1/ƒ

Dans les conditions de Gauss où les rayons sont paraxiaux,
on symbolise donc les mirois sphériques comme ci-contre:
L'utilsation de ces symboles permet donc
de confondre FS avec FS cos β.
|