Mathématiques 2: Géométrie
Les angles
Le sextant
1. Définition
Un sextant est un instrument servant à mesurer
l'angle observé entre deux points.
De façon détaillée, un sextant est un instrument servant à mesurer
la distance angulaire entre deux points quelconques
aussi bien verticalement qu'horizontalement.
Il est souvent utilisé pour relever la hauteur angulaire d’un astre
au-dessus de l’horizon, comme la hauteur angulaire du soleil .
Le sextant était utilisé dans l’aéronautique et la marine. Actuellement,
son usage est restreint en raison du développement des systèmes de positionnement
par satellites, comme le GPS.
Le sextant a été inventé vers les années 1730. Il a remplacé l’astrolabe
et l’octant qui étaient déjà utilisés à l’époque de la Grèce Antique.
2. Constitution d'un sextant
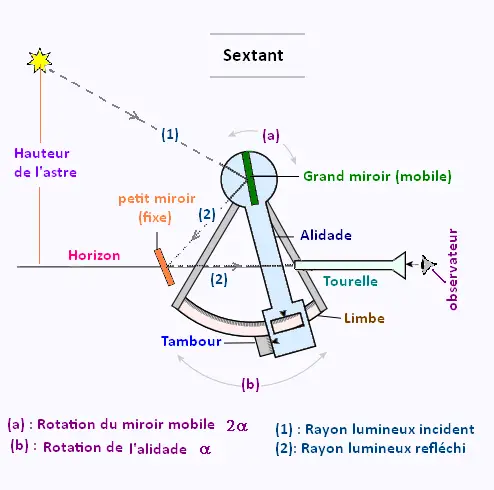Un sextant est composé principalement de:
• un petit miroir fixe ( miroir de gauche: transparent et
refléchissant),
• un grand miroir mobile ( miroir de droite: refléchissant),
• une alidade: un levier qui fait tourner le grand miroir,
• un arc de cercle gradué: le limbe,
• une lunette de visée parallèle à l’horizon
Le tambour sert à ajuster la précision de l’instrument.
Le miroir fixe est parallèle à l’alidade lorsqu’elle est en position
zéro (0°).
Le petit miroir fixe de gauche est composé de deux parties: la moitié
gauche est transparente et la moitié droite est réfléchissante. Cela
permet à l’observateur de voir en même temps l’horizon et l’astre.
L’angle du secteur circulaire qui forme le sextant mesure 60°, ainsi
cet appareil est nommé sextant.
L'octant comporte un arc gradué de 45o et permet
de mesurer des angles de 90o. 45o représente 1/8
des 360o du cercle complet d’où le nom d’octant.
L'octant a été remplacé par le sextant.
Afin de faciliter l'utilisation de l'appareil, les graduations du limbe sont
doublées c'est à dire que chaque demi-degré compte pour un degré.
3. Fonctionnement d'un sextant
• Le grand miroir mobile est fixé à l’alidade dont le point d’attache
se trouve au sommet de l’appareil. Ce miroir réfléchit la lumière
provenant des astres vers le miroir fixe (m). Le levier indique alors
un angle sur l’arc de cercle gradué. Cet angle est la moitié de l’élé-
vation de l’astre.
• Le petit miroir doit être parfaitement parallèle au grand pour
ainsi renvoyer l’image de l’horizon.
• Pour mesurer l’élévation d’un astre, il suffit de déplacer l’alidade (et
donc le grand miroir M jusqu’à ce que l’image de l’astre concorde
avec la ligne d’horizon.
4. Relation entre les deux angles de
rotation
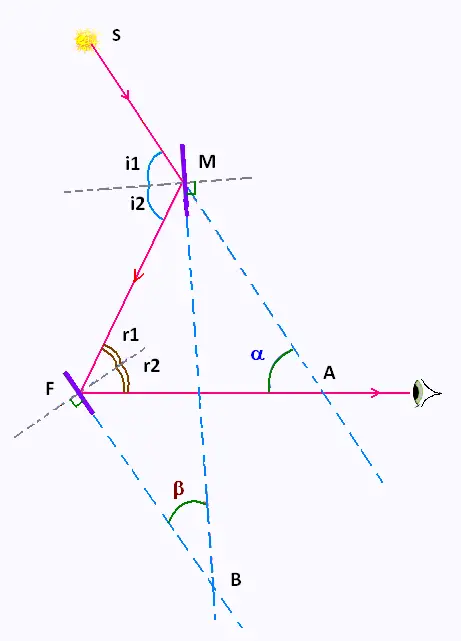
Le rayon lumineux SM venant de l'astre S frappe le miroir "M" avec un angle
d'incidence i1. Il se réfléchit suivant l'angle i2 et vient frapper le miroir "F"
en son centre.
Ce rayon lumineux arrive sur le petit miroir "F" avec un angle d'incidence r1,
puis se réfléchit vers la lunette, suivant l'angle r2.
D'après la Loi de la réflexion « l’angle d’incidence est égal à l’angle de réflexion»,
on a: i1 = i2 et r1 = r2.
L'angle α est l'angle entre l'horizon est la direction de l'astre
S au miroir M, c'est à dire i1.
L'angle que font entre eux les deux miroirs M et F est β. C'est l'angle
dont on a tourné le grand miroir M lorsque l'observateur a assuré la coïncidence
de l'image doublement réfléchie de l'astre et de l'image directe de l'horizon.
• Dans le triangle BMF:
α + (180o - i1 - i2) + r1 + r2 = 180o
α + 180o - 2i1 + 2r1 = 180o
α = 2i1 - 2r1 = 2(i1 - r1)
α = 2(i1 - r1) (1)
• Dans le triangle AMF:
β + (90o - i2) + r1 + 90o = 180o
β - i2 + r1 = 0
β = i2 - r1 = i1 - r1 (2)
β = i1 - r1 (2)
Les relations (1) et (2) donnent :
α = 2 β
|
