Calculus of Variations:
Functionals
Principle of Least Action
Lagrangian formalism
The Atwood machine

The Atwood machine

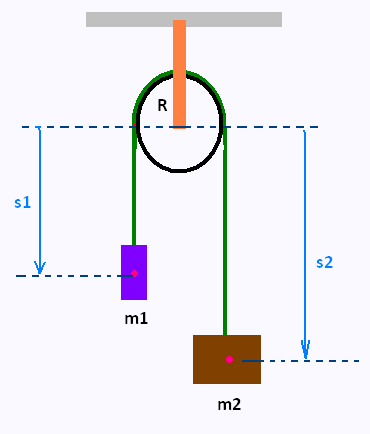
In this example, we compute the equation of motion of the Atwood machine.

The simplest version ofthe Atwood machine consists of two masses, m1 and m2, suspended on either side of a massless, frictionless pulley of radius R, by a massless rope of length l.

Let's take the origin in space at the center of the pulley. The vertical position of m1, is the distance s1 from the origin. The vertical position of m2, is the distance s2 from the origin.

We have

s1 + πR + s2 = l

So s2 = l - s1 - πR

The velocity of m1 is s' = ds/dt , and the velocity of m2 is - s' = - ds/dt. The kinetic energy of the system (the two masses) is then

T = (1/2)(m1 s'² + m2(- s')²) = (1/2)s'² (m1 + m2)

T = (1/2)s'² (m1 + m2)

The potential energy is

V = - m1gs - m2(l - πR - s) = -(m1 - m2)gs + (const.).

We drop the additive constant because only the derivative of V will be needed to make the EL equation.

V = -(m1 - m2)gs

We have then

L(s, s') = T - V = (1/2)s'² (m1 + m2) + (m1 - m2)gs

L(s, s') = (1/2)s'² (m1 + m2) + (m1 - m2)gs

So the equation of motion is

∂L/∂s - d[∂L/∂s']/dt = 0

That is

(m1 - m2)g - (m1 + m2)s" = 0

or

s" = (m1 - m2)g/(m1 + m2)

s" = (m1 - m2)g/(m1 + m2)

This is the result we get by Newton’s second law. The Lagrangian formalism is simpler than the Newtonian approach.