Variational Methods
Contents
Euler Lagrange Equation
Lagrangian Mechanics
Application
© The scientific sentence. 2010
|
|
Functionals:
Variational Methods
Euler-Lagrange equation
Euler-Lagrange equation
From the functional S[y] defined by the integral:
S[y] = ∫ x1x2 f(y(x), y'(x), x) dx
and by using the variational approach, we will determine
the Euler-Lagrange equation .
Let's suppose that we know the function yo(x), which makes
the functional S extremal; that is S[yo] is a point extremum.
Since S[yo] is stationary, a small variation η(x) of the function y(x) around yo(x) involves a variation δS = 0, at the first order in η(x). That is:
y(x) = yo(x) + η(x)
Where η(x) << yo(x) for any x .
We will calculate the induced variation of the functional for
a fixed value of x:
δS[y] = ∫ x1x2 δf(y(x), y'(x), x) dx =
∫ x1x2 [f(y(x), y'(x), x) - f(yo(x), y'o(x), x)] dx =
∫ x1x2
f(yo(x) + η(x), yo'(x) + η'(x), x) -
f(yo(x), yo'(x), x)
In the first order in η(x) and η'(x), we have the
following first terns of the Taylor series:
f(y(x), y'(x), x) =
f(yo(x), yo'(x), x) + (1/!1)(y - yo)∂f/∂y + (1/!1)(y' - yo')∂f/∂y' =
f(yo(x), yo'(x), x) + η(x)∂f/∂y + η'(x)∂f/∂y'
Therefore:
δS[y] = ∫ x1x2 [f(y(x), y'(x), x) - f(yo(x), y'o(x), x)] dx =
∫ x1x2 [f(yo(x), yo'(x), x) + η(x)∂f/∂y + η'(x)∂f/∂y'
-
f(yo(x), y'o(x), x)] dx =
∫ x1x2 [ η(x)∂f/∂y + η'(x)∂f/∂y'
] dx .
δS[y] = ∫ x1x2 [η(x)∂f/∂y + η'(x)∂f/∂y'
] dx
The integration by part of the second term is:
∫ x1x2 [η'(x)∂f/∂y'
] dx = [η(x)∂f/∂y']x1x2 -
∫ x1x2
η(x) d[∂f/∂y']/dx
Therefore:
δS[y] = ∫ x1x2[
η(x)∂f/∂y - η(x) d[∂f/∂y']/dx] dx +
[η(x)∂f/∂y']x1x2.
Since y(x1) and y(x2) are fixed, η(x1) = η(x2) = 0 and the
last term of the equation vanishes. It remains :
δS[y] = ∫ x1x2
η(x)[∂f/∂y - d[∂f/∂y']/dx] dx
As δS = 0, regardless η(x), we obtain:
∫ x1x2
η(x)[∂f/∂y - d[∂f/∂y']/dx] dx = 0
∂f/∂y - d[∂f/∂y']/dx = 0
This is the Euler-Lagrange equation.
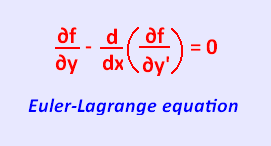

|
|