Variational Methods
Contents
Euler Lagrange Equation
Lagrangian Mechanics
Application
© The scientific sentence. 2010
|
|
Functionals:
Variational Methods
Euler-Lagrange equation simplified
Beltrami formula
1. The other form of Euler-Lagrange equation
Here is the Euler-Lagrange equation:
∂f/∂y - d[∂f/∂y']/dx = 0
.
For the second term, the total differential is:
d[∂f/∂y'] = ∂[∂f/∂y']/∂y dy +
∂[∂f/∂y']/∂y' dy' + ∂[&partf/∂y']/∂x dx =
(∂2f/∂y'∂y)dy +
(∂2f/∂y'2)dy' + (∂2f/∂y'∂x)dx.
Threfore:
d[∂f/∂y']/dx =
(∂2f/∂y'∂y)y' +
(∂2f/∂y'2)y" + ∂2f/∂y'∂x .
If the functional f does not depend explicitly on x, that is
∂f/∂x = 0 ; the last term in the latter equation vanishes,
and the differential becomes:
d[∂f/∂y']/dx =
(∂2f/∂y'∂y)y' +
(∂2f/∂y'2)y" .
Therefore, the Euler-Lagrange equation becomes.
∂f/∂y - (∂2f/∂y'∂y)y' -
(∂2f/(∂y')2)y" = 0
∂f/∂y - (∂2f/∂y'∂y)y' -
(∂2f/∂y'2)y" = 0
2. Euler-Lagrange equation simplified
On the other hand, we have :
d[f - y'(∂f/∂y')]/dx =
(∂f/∂y) y' +
(∂f/∂ y')y" + ∂f/∂x
- y"(∂f/∂y') - y'[(∂2f/∂y'∂y)y'
+ (∂2f/∂y'2)y" + (∂2f/∂y'∂x)
]
=
(∂f/∂y) y'+ (∂f/∂y')y"
- y"(∂f/∂y') - (∂2f/∂y'∂y)y'2
- (∂2f/∂y'2)y"y'
]
=
y' [(∂f/∂y)
- (∂2f/∂y'∂y)y'
- (∂2f/∂y'2)y"]
According to the above second form of Euler-Lagrange equation, the sum of the terms between the brackets is equal to zero, therefore:
d[f - y'(∂f/∂y')]/dx = 0 . So
If the functional f does not depend on x,
that is
∂f/∂x = 0 , then:
d[f - y'(∂f/∂y')]/dx = 0
This is the simplified Euler-Lagrange equation. We can express it as
f - y'(∂f/∂y') = constant.
called Beltrami formula.
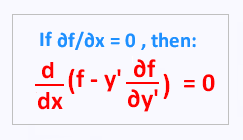
|
|