Functionals:
Lagrangian Mechanics
Hamiltonian Principle of Least Action

1. Principle of Least Action

The results of variational calculus allowed us to formulate the Euler-lagrange equation.

∂f/∂y - d[∂f/∂y']/dx = 0

By specifying the functional f as the Lagrangian, we could write:

L(q(t), q'(t), t) = T - V = 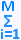(1/2)m q'_i² - U(q₁(t), q₂(t), . . . q_M) .

The Hamiltonian Principle of Least Action is:

The trajectory of a particle described through the Newtonian equations of motion is an extremal of action integral.


Indeed, Lagrange's equations

m q_i" = ∂U/∂q_i
i = 1, 2, ..., M

wich are the Newtonian equations come from that the fonction of the functional is the lagrangian
L(q(t), q'(t), t) = 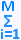(1/2)m q'_i² - U(q₁(t), q₂(t), . . . q_M)

and from the Euler-Lagrange equation

∂f/∂y - d[∂f/∂y']/dx = 0

which comes, via variational calculus, from the fact that the functional, here action integral :

S[q(t)] = ∫ _t1^t2 L(q(t), q'(t), t) dt is minimized.

2. Other ways to read the Hamilton's principle

The classical motion of a particle is described by the minimal of its action integral.

If, at the instants t1 and t2, the system occupies respectively two positions q1 and q2, exactly defined, then between these two instants its evolution is such that its action integral S = ∫L(q,q',t) is extremal.