Calculus of Variations:
Functionals
Principle of Least Action
The shortest path

The shortest path

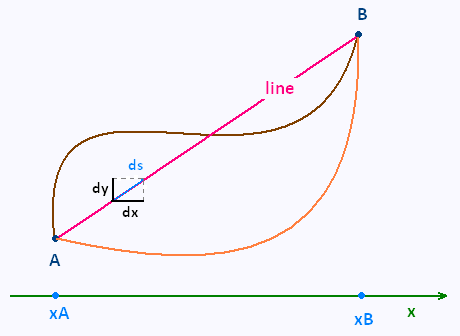
We search for the path y(x) that minimizes the length l(y):

l(y) = ∫_x1^x2 f(y') dx

which obeys Euler–Lagrange equation.

The function f depends only on the element of the path ds, hence on y' = dy/dx.

We have then

f(y') = ds/dx = [dx² + dy²]^1/2/dx =
[1 + (dy/dx)²]^1/2 = [1 + y'²]^1/2

with y(xA) = y(xB) = constant.


Euler equation reads:

∂f/∂y - d[∂f/∂y']/dx = 0

Since f does not depend on y, we have ∂f/∂y = 0 , hence

d[∂f/∂y']/dx = 0     or     ∂f/∂y' = constant.

∂f/∂y' = (1/2)[1 + y'²]^-1/2 (2 y') = y'[1 + y'²]^-1/2

We have then y'[1 + y'²]^-1/2 = constant. Therefore y' = constant

y' = constant     or     y = a x + b

That is, the equation of the ligne that passes by the points A and B.