Variational Methods
Contents
Euler Lagrange Equation
Lagrangian Mechanics
Application
© The scientific sentence. 2010
|
|
Functionals:
Lagrangian Mechanics
Lagrange's equations
Lagrange equation
Here is the Euler-Lagrange equation:
d[∂f/∂y']/dx = ∂f/∂y
.
In Classical Mechanics, this equation takes the general expression:
d[∂L/∂qi']/dt = ∂L/∂qi
.
q(t) is the trajectory of a system of one particle of M degrees of freedom described by the configurational coordinates q(t) = (q1(t), q2(t), . . . qM(t)) with respect to the time t. In case of N classical particles holds M = 3N.
The function L is the Lagrangian; function of the variable positions
q, the velocities q', and the time t related to the system.
L = L(q(t), q'(t), t) = 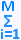 KE(i) - PE(i)
.
KE(i) and PE(i) are respectively the kinetic energy and
the potential energy of the system.
This formula is expressed as:
L(q(t), q'(t), t) =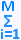
(1/2)m q'i2 - U(q1(t), q2(t), . . . qM)
.
The Lagrangian equation takes then the following expression:
m qi" = ∂U/∂qi
i = 1, 2, ..., M
In Classical Mechanics, Lagrange's equation is:
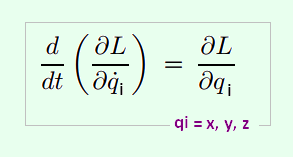
More simplified, it reads:
|
|
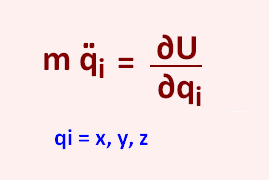
