Variational Methods
Contents
Euler Lagrange Equation
Lagrangian Mechanics
Application
© The scientific sentence. 2010
|
|
Calculus of Variations:
Functionals
Principle of Least Action
Pendulum
Pendulum
In this example, we will use the Lagrangian formulalism
to determine the equation of a simple pendulum.
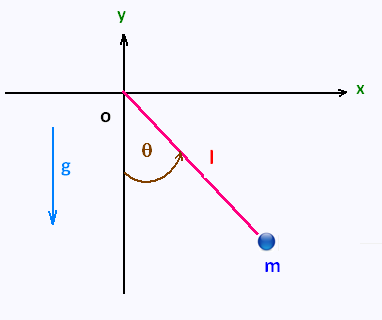
Let's consider a pendulum composed of an object
of mass m and a massless string of length l in a constant
gravitational field with acceleration g.
The motion of the pendulum is two-dimensional. It can be
reduced to the a one-dimentional motion by using a single
generalized coordinate which is the angle θ
measured from the negative y-axis, such the position of
the object is given as:
x (θ) = l sin θ
y (θ) = - l cos θ
with associated velocity components
x'(θ, θ') = l cos(θ) θ'
y'(θ, θ') = l sin(θ) θ'
Hence, the kinetic energy of the pendulum is
KE = (m/2) (x'2 + y'2) =
ml2 θ'2/2.
KE = (ml2/2) θ'2
and choosing the zero potential energy point when
θ = 0, the gravitational potential energy is
PE = mgl(1 - cos θ).
PE = mgl(1 - cos θ)
The Lagrangian L = KE - PE is, therefore, written as
L(θ,θ') = (ml2/2)θ' 2
- mgl(1 - cos θ)
and the Euler-Lagrange equation for θ is
∂L/∂θ' = ml2θ'. So
d(∂L/∂)/dt = ml2θ"
∂L/∂θ = - mgl sin θ
Therefore
ml2 θ" = - mgl sin θ
or
θ" + (g/l) sin θ = 0
θ" + (g/l) sin θ = 0
That is the differential equation of a simple pendulum
of period T = 2π √(l/g)
|
|