Variational Methods
Contents
Euler Lagrange Equation
Lagrangian Mechanics
Application
© The scientific sentence. 2010
|
|
Calculus of Variations:
Functionals
Principle of Least Action
The shortest path
The shortest path
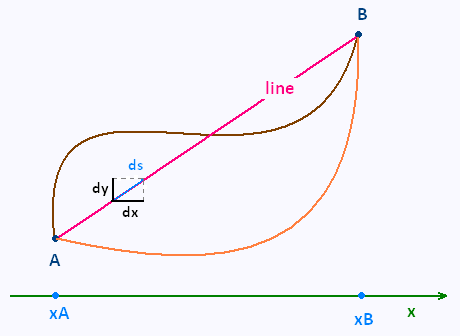
We search for the path y(x) that minimizes the length l(y):
l(y) = ∫x1x2 f(y') dx
which obeys Euler�Lagrange equation.
The function f depends only on the element of the path ds, hence on
y' = dy/dx.
We have then
f(y') = ds/dx = [dx2 + dy2]1/2/dx =
[1 + (dy/dx)2]1/2 = [1 + y'2]1/2
with y(xA) = y(xB) = constant.
Euler equation reads:
∂f/∂y - d[∂f/∂y']/dx = 0
Since f does not depend on y, we have ∂f/∂y = 0 , hence
d[∂f/∂y']/dx = 0 or
∂f/∂y' = constant.
∂f/∂y' = (1/2)[1 + y'2]-1/2 (2 y') =
y'[1 + y'2]-1/2
We have then y'[1 + y'2]-1/2 = constant. Therefore
y' = constant
y' = constant or
y = a x + b
That is, the equation of the ligne that passes by the points A and B.
|
|