1. Newton's rings

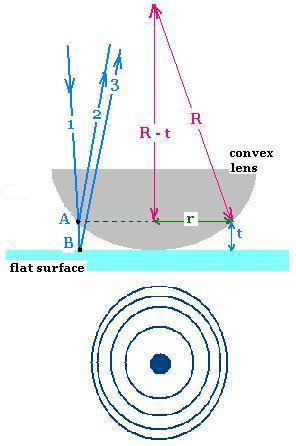The device to prodice Newton's rings contains A flat surface, a convex lens (spherical surface) with an air wedge formed between them. The lens is illuminated with normally incident monochromatic light (ray 1). The circular fringes viewed are concentric circles around the point of contact with the flat surface.

R is the radius of curvature of the lens, T is the thickness of the lens where we choose r.

Pythagorean theorem gives:
r² + (R - t)² = R²

Therefore
r² + t² - 2 R t = 0

Because it is small, we neglect the term t², hence:
r² = 2 R t , or
t = r²/2R

t = r²/2R    (1)

At the point A, th reflected ray does not undergo a phase change, but at the point B the reflected ray 2 undergoes a π phase change.

Therefore
Δφ = φ3 - φ2 = (φB + φ(t)) - φA

The path difference between reflected rays is δ = 2t
φ(t) = 2 π δ/λ = 4 π t/λ

Hence:
Δφ = (π + (4πt/λ)) - o =
π(1 + (4t/λ))

1.The bright fringes corresponds the constructive interferences and a phase difference of 2 m π. That is:
2 m π = π(1 + (4t/λ))

Hence:
2 m = (1 + (4t/λ)), or:
t = (2 m - 1)λ/4

t = (2 m - 1)λ/4    (2)

2. The dark fringes corresponds the desstructive interferences and a phase difference of (2 m + 1) π. That is:
(2 m + 1) π = π(1 + (4t/λ))

Hence:
2 m = 4t/λ), or:
t = mλ/2

From equation (1), the radius r of the m-th ring corresponds to the thickness of the air wedge t :

r = (2 R t )^1/2

The bright m-th ring corresponds to
r = (2 R t )^1/2 = [R (m - 1/2)λ]^1/2    (3)

The dark m-th ring corresponds to
r = (2 R t )^1/2 = (R mλ)^1/2    (4)

The bright m-th ring corresponds to:
r = [R (m - 1/2)λ]^1/2
The dark m-th ring corresponds to:
r = (R mλ)^1/2

Remarks:

1. The index of refraction of the lens has no importante.
2. The index of refraction of air is n = 1 that gives:
λ (in air) = λ(in vacuum) = λ

2. Example

If the incident light has a lambda; = 500 nm, and R = 2.00 m, what is the radius of the 4th bright ring ?

r = [R (m - 1/2)λ]^1/2 =
[2.00 (4 - 1/2)5 x 10 ^-7>]^1/2 =
18.71 x 10 ^-4> m = 1.9 mm.