Deviation by a parallel sheet

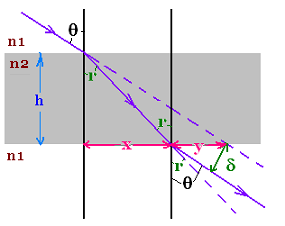
    A light ray is refracted at the surface (interface) n1-n2, crosses the parallel sheet of thickness "h", and emerges at the surface n2-n1. The incidence angle is θ. we are interested to know the deviation δ.

First, the ray emerges parallel to the incident ray. Indeed, according to Snell's law, for the interface n1-n2, n1 sin θ = n2 sin r; and for the interface n2-n1, n2 sin r = n1 sin (angle of emergence). Therefore, angle of emergence = θ and the incidence ray is parallel to the emerged ray.

We have:
x = h tan r
x + y = h tan θ
Then:
y = h tan θ - x = h tan θ - h tan r
Substituting in this relationship the expression of sin r taken from Snell's law, n1 sin θ n2 sin r → sin r = (n1/n2) sin θ, we obtain:

y = h tan θ - x = h tan θ - h sin r/ cos r
= h tan θ - h sin r/ (1 - sin²r)^1/2
= h tan θ - h (n1/n2) sin θ)/ (1 - [(n1/n2) sin θ]²)^1/2
= h tan θ [1 - (n1/n2) cos θ/ (1 - [(n1/n2)² sin² θ])^1/2]

y = h tan θ [1 - (n1/n2) cos θ/ (1 - [(n1/n2)² sin² θ])^1/2]

We have also: δ = y cos θ. Then, finally,
δ = h sin θ [1 - (n1/n2) cos θ/ (1 - [(n1/n2)² sin² θ])^1/2]

δ = h sin θ [1 - (n1/n2) cos θ/ (1 - [(n1/n2)² sin² θ])^1/2]