1. Fermat's Principle:
Fermat (1601-1665) stated the principle of least time for a light ray: The time is
minimum for a light ray to travel between
two points with respect to nearby pahs.
Here are two examples: the first
confirms the reflection principle; and the second the refraction principle of
Geometrical Optics.
2. Fermat's Principle: Reflection
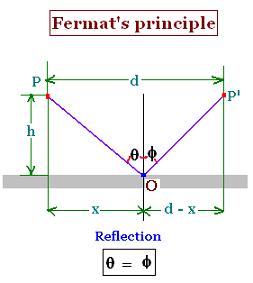
path = PO + OP'
= path1 + path2 = v x time1 + v time2 = v(time1 + time2);
"v" is the speed of light in the the related medium.
path =
= [x2 + h2]1/2 +
[( d- x)2 + h2]1/2
The related nearby paths are: "x "and "d - x".
The time minimum id given by the derivative, set equal zero,
of the time with respect to the variable "x".
Let's write:
d(time)/dx = 0; that yields, assuming that the speed of the light
ray is constant:
d(time)/dx = d(path/v)/dx = d(path)/dx = 0
d([x2 + h2]1/2 +
[( d - x)2 + h2]1/2)/dx
= 0
= 2x [x2 + h2]- 1/2 +
- 2(d - x)[(d - x)2 + h2]- 1/2
Then:
x [x2 + h2]- 1/2 =
(d - x)[( d - x)2 + h2]- 1/2
We have:
sin θ = x [x2 + h2]- 1/2 and
sin Φ = (d - x)[(d - x)2 + h2]- 1/2
Thus:
sin θ = sin Φ so θ = Φ
Conclusion:
Using Fremat's principle leads to the first principle of Geometrical Optics,
that is the angle of incidence is equal to the angle of
reflection.
3. Fermat's Principle: Refraction
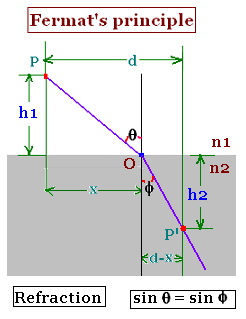
path = PO + OP'
= path1 + path2 = v1 x time1 + v2 x time2, with v1 and v2
are the speed of the ray light in the medium n1 and the medium n2
respectively.
parth =
= [x2 + h12]1/2 +
[( d- x)2 + h22]1/2
The related nearby paths are: "x "and "d - x".
The time minimum id given by the derivative, set equal zero,
of the time with respect to the variable "x".
Let's write:
d(time)/dx = 0; that yields, assuming that the speed of the light
ray is constant in the two media:
d(time)/dx = d(path1/v1)/dx + d(path2/v2)/dx = 0
d([x2 + h12]1/2 +
[( d - x)2 + h22]1/2)/dx
= 0
= (1/v1)2x [x2 + h12]- 1/2 +
- (1/v2) 2(d - x)[(d - x)2 + h22]- 1/2
Then:
(1/v1) [x2 + h12]- 1/2 =
(1/v2) (d - x)[( d - x)2 + h22]- 1/2
Using the definition of the index of refraction of a medium, we have:
n1 = c/v1 and v2 = c/v2; thus:
n1 x [x2 + h12]- 1/2 =
n2 (d - x)[( d - x)2 + h22]- 1/2
We have:
sin θ = x [x2 + h12]- 1/2 and
sin Φ = (d - x)[(d - x)2 + h22]- 1/2
Thus:
n1 sin θ = n2 sin Φ
Conclusion:
Using Fremat's principle leads to the second principle of Geometrical Optics,
that is Snell's law.