1. Image formed by a plane reflecting mirror

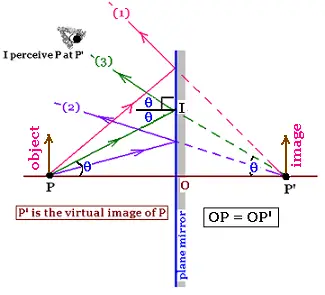
We perceive the image of an object "P" bacwards the mirror by the diverging rays from the miror. The image is obtained by projeting rays that converge at the point "P'". This image is virtual.

If we consider the ray (3), its reflection gives the angle θ at the point I. Then the angle PP'I is equal to θ (corresponding angles). Thus, the triangle PP'I is isocele. The line IO which is the height is then the bisectrix of this triangle. Therefore PO = OP' and PP' is perpendicular to IO. The object and the image are at the same distance from the mirror.

The image of the obect is erect (right side).

2. Mirror equation

Curved mirrors are also used to form the image of an object. there are concave spherical or convex spherical mirrors.
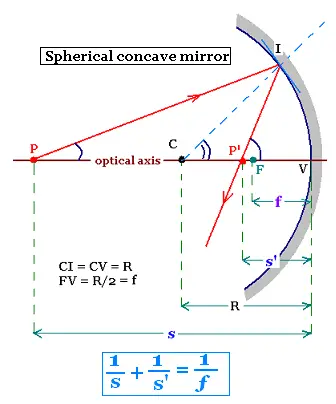
Let's consider a concave mirror of center C and radius of curvature R. The ray PI is reflectef at the point I and then crosses the optical axis at the poit P'. CI = CV = R, where V is the vertex of the spherical mirror. The line joininig P (object), C center of the C, and the vertex is called optical axis. The light rays that are not close to the optical axis blur (spherical aberration) the image of an object conversely of the rays close to the optical axis called paraxial rays. In Geometrical Optics, we always use only these rays.

The angles <PIC and <CIP' are equal because the ray IP' is the reflected ray and the line IC is normal to the tangent fo the cercle.

<PIP' = 2 <PIC
CPI + 2<CIP = IP'V (the exterior angle of a triangle is the sum of the two opposite inteior angles) Similarly,
CPI + CIP = ICV.
We have then:
<CPI + 2<CIP = <IP'V
<CPI + <CIP = <ICV

Eliminating the angle CIP, we find:
<CPI + <IP'V = 2 <ICV     (1)

For paraxial rays, all these angles are small, they are the equal to their radian measures, we can then write:
<CPI = IV/s
<CIP = IV/s'
<ICV = IV/R

The relationship (1) becomes:
IV/s + IV/s'= 2 IV/R
or
1/s + 1/s'= 2/R     (2)
If the object is placed at a far distance (infinity) from thr mirror, the length s becomes large, so 1/s becomes small and neglected. Then s' = R/2 which means all the reflected rays pass through the point F. The point F is called the focal point of the mirror. It is placed at the diatance VF from the vertex. This distance is equal to ƒ = R/2, called focal length of the mirror.

Rewriting the relationship (2), it becomes:
                1/s + 1/s'= 1/ƒ     (3)
That is the mirror equation.

3. image formed by reflecting spherical mirrors: Mirror ray tracing

3.1. Magnification of an optical system

The magnification "m" of an optical system is the ratio of the image size to the object size.

3.2. Concave mirror

There are three principal ray to trace to obtain the image of an object by graphical construction:

(1). The incident parallel ray to the optical axis reflets to pass through the focal point.
(2). The incident ray passing by the focal point reflets parallel to the optical axis.
(3). The incident ray passing by the center of curvature of the mirror reflects back ton itself.
(0). The ray (0) is optional. It just shows the first law of reflection.

3.2.1. The object is far from the mirror

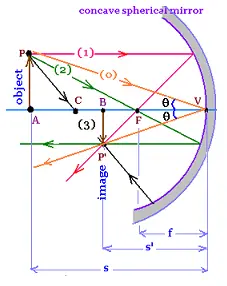
The object is far from the mirror:(FA >> FV). The rays from the object converge, then the image is real. The image is inverted , then the magnification is negative:
BP'V and APV are similar, then:

m = BP'/AP = - s'/s



3.2.2. The object is between the vertex and the focal point of the mirror

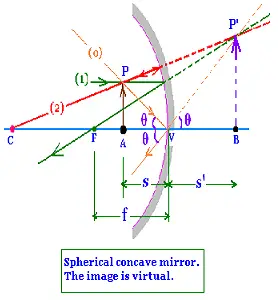
The object is located between the mirror and its focal point:(FA < FV). The ray from the obect diverge, then he image is virtual. The image is right side up , then the magnification is positive.
BP'V and APV are similar, then:

m = BP'/AP = + s'/s

3.3. Convex mirror

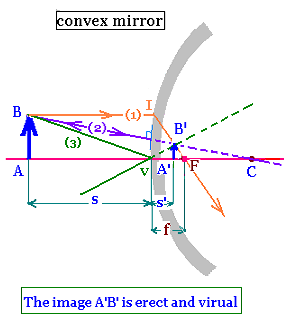
Two points are required to trace the image of the object. Ray (1) parallel to the optica axis before reflection and diverges from the focal point F after reflection; and ray (2) passing trough the centre of curvature of the sphere and reflects back on itself. The image A'B' of the object AB is pointed to the intersection of these rays.

For the convex mirror, we have also the mirror equation:
1/s + 1/s' = 1/f, and
m = s'/s

Indeed,
- The two triangles VAB and VA'B' are similar; then:
m = A'B'/AB = s'/s     (1)

- The ywo triangles FVI and FA'B' are similar; then:
m = A'B'/VI = A'B'/AB = (f - s')/f     (2)

The relationships (1) and (2) gives:
s'/s = (f - s')/f, so
fs' = sf - ss' or f (s - s') = ss'. Then
1/f = (s - s')/ss' = 1/s' - 1/s

f is negative, s' is also negative.
Therefore: 1/f = 1/s + 1/s'

4. Convention used for spherical mirrors

The position of an object and image is positive if they are real; negative if they are virtual. The focal length is positive in concave and negative in convex mirrors.