Geometrical Optics:
Geometrical Optics & Physics Optics.
a
Huygens Principle:
Wavefronts.
a
Reflection:
The first law of Geometrical Optics.
a
Refraction:
The second law of Geometrical Optics: Snell's law.
a
Critical angle:
Internal total reflection.
a
images formed by reflection
Spherical concave mirrors. Mirror equation.
a
images formed by refraction
Spherical convex mirrors ..
a
Fermat's principle:
Fermat's principle for reflection and refraction..
a
lenses:
Thin lenses and Lens-makers' equation ..
a
prism:
Prism, colors minimum deviation ..
a
Human eye:
near point, far point, nearsightedness, farsightedness..
a
Microscope:
Microscope: simple, compound, and magnification..
a
Telescope:
Telescope: magnification..
a
Resolution:
optical microscope, electron microscope ..
a
dispersion:
dispersion, more about the refractive index, and colors of a prism ..
a
parallel sheet:
deviation by a parallel sheet ..
a
thin films :
thin films and Newton's rings..
a
Newton's rings:
thin films and Newton's rings..
a
Descartes rainbow:
Primary and secondary rainbows ..
a
Some applications
More fun with Optics ..
a
Optics calculator:
Optics calculator: all the related calculations ..
a
home
The fundamental, and just this ..
a
scientificSentence
a

__________________
a

Geometrical Optics: Fermat's Principle
Optics -     Geometrical Optics..




1. Fermat's Principle:

      Fermat (1601-1665) stated the principle of least time for a light ray: The time is minimum for a light ray to travel between two points with respect to nearby pahs.

Here are two examples: the first confirms the reflection principle; and the second the refraction principle of Geometrical Optics.



2. Fermat's Principle: Reflection


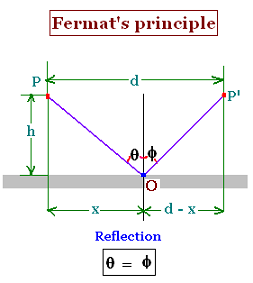
path = PO + OP'
= path1 + path2 = v x time1 + v time2 = v(time1 + time2); "v" is the speed of light in the the related medium.

path = = [x2 + h2]1/2 + [( d- x)2 + h2]1/2

The related nearby paths are: "x "and "d - x".

The time minimum id given by the derivative, set equal zero, of the time with respect to the variable "x". Let's write:
d(time)/dx = 0; that yields, assuming that the speed of the light ray is constant:
d(time)/dx = d(path/v)/dx = d(path)/dx = 0
d([x2 + h2]1/2 + [( d - x)2 + h2]1/2)/dx = 0
= 2x [x2 + h2]- 1/2 + - 2(d - x)[(d - x)2 + h2]- 1/2

Then:
x [x2 + h2]- 1/2 = (d - x)[( d - x)2 + h2]- 1/2

We have:
sin θ = x [x2 + h2]- 1/2 and
sin Φ = (d - x)[(d - x)2 + h2]- 1/2

Thus: sin θ = sin Φ so θ = Φ

Conclusion:
Using Fremat's principle leads to the first principle of Geometrical Optics, that is the angle of incidence is equal to the angle of reflection.



3. Fermat's Principle: Refraction


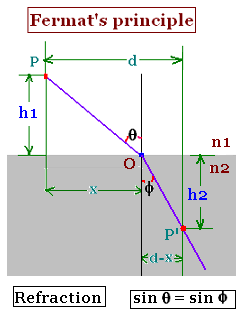
path = PO + OP'
= path1 + path2 = v1 x time1 + v2 x time2, with v1 and v2 are the speed of the ray light in the medium n1 and the medium n2 respectively.

parth = = [x2 + h12]1/2 + [( d- x)2 + h22]1/2

The related nearby paths are: "x "and "d - x".

The time minimum id given by the derivative, set equal zero, of the time with respect to the variable "x". Let's write:
d(time)/dx = 0; that yields, assuming that the speed of the light ray is constant in the two media:
d(time)/dx = d(path1/v1)/dx + d(path2/v2)/dx = 0
d([x2 + h12]1/2 + [( d - x)2 + h22]1/2)/dx = 0
= (1/v1)2x [x2 + h12]- 1/2 + - (1/v2) 2(d - x)[(d - x)2 + h22]- 1/2

Then:
(1/v1) [x2 + h12]- 1/2 = (1/v2) (d - x)[( d - x)2 + h22]- 1/2

Using the definition of the index of refraction of a medium, we have: n1 = c/v1 and v2 = c/v2; thus:
n1 x [x2 + h12]- 1/2 = n2 (d - x)[( d - x)2 + h22]- 1/2

We have:
sin θ = x [x2 + h12]- 1/2 and
sin Φ = (d - x)[(d - x)2 + h22]- 1/2

Thus: n1 sin θ = n2 sin Φ

Conclusion:
Using Fremat's principle leads to the second principle of Geometrical Optics, that is Snell's law.



 
Custom Search

© 2009. The scientificsentence . All rights reserved.