1. Thin films
Thin film is a thin layer of substance between two
other media, such as an oil spot on the road, or a soap
bubble in air. A light incident in a thin film produces
various colors, that is several wavelengths. The observed
colors result from the interference of the waves (rays)
reflected from the two opposite surfaces of the film.
The color of the patterns depends on the wavelength
of the wave, and the thickness and the index of
refraction of the film.
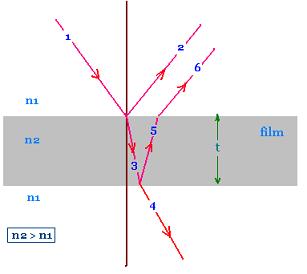
Consider a thin film of thickness t and index of refraction n2. For
simlicity, we assume that the light rays are nearly normal to the two
surfaces of the film.
We will use the following facts:
The reflected electromagnetic wave traveling from a medium of index of
refraction n1 toward a medium of index of refraction n2 undergoes a π
phase change when n2 > n1; but there is no phase change in the
reflected wave if n2 < n1.
The wavelength λ of a wave in vacuum is equal to λ/n
in a medium of index of refraction n.
On the point A, the ray 1 udergoes a phase change of π, because n2 > n1.
It reflects and gives the ray 2.
On the point B, the refracted ray 3 is reflected to the ray 5
and undergoes not phase change, because n1 < n2. The ray 5 is
refracted and emarges from the film witout
phase change because there is no phase change with refraction.
(only with reflection).
Therefore the difference in phase for the reflected rays 6 and the
ray 2 is :
Δφ = φ2 - φ1 = (φB + φ(2t)) - πA =
( 0 + (2π 2 tn/λ)) - π = π(4 t n/λ - 1)
Δφ = π[4 t n/λ) - 1]
Δφ = π[(4 t n/λ) - 1]
1.1. Thin films: constructive interference
To have constructive interference, the two rays 2 and 6 will
satisfy the condition:
Δφ = 2m π
where m is an integer
Hence
Δφ = π(4 t n/λ - 1) = 2 m π
Then:
t = (2m + 1)λ/4n
constructive interference:
t = (2m + 1)λ/4n
1.2. Thin films: destructive interference
To have desstructive interference, the two rays 2 and 6 will
satisfy the condition:
Δφ = (2m + 1) π
where m is an integer
Hence
Δφ = π(4 t n/λ - 1) = (2m + 1) π
Then:
t = (2m + 2)λ /4n = (m + 1)λ /2n
destructive interference:
t = (2m + 2)λ /4n = (m + 1)λ /2n
1.3. Example: variable thickness
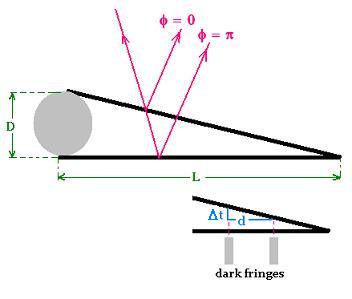
For destructive interference, the width between
two dark fringes is equal to =
Δt = λ /2n
The triangles with (D,L) and (Δe, d) are similar, then:
Δt/d = D/L
Therefore:
D = L Δt/d = L λ /2n d
D = L Δt/d = L λ /2n d
|


