Simple and compound microscope
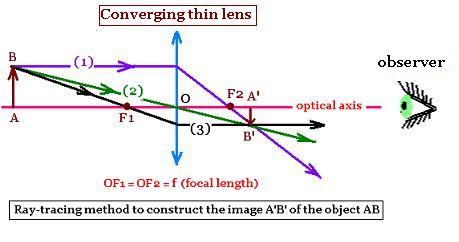
We want to form the image of an object seen through a converging
lens. If the object is placed at left infinity, its image will be located
exactly at the right focal point. If the object is placed at the
left of the focal point of this converging lens, the related image
is real and inverted. The more we approch to this point from the left,
the more the related image is large, and more far from the lens. If it
is placed exactly at the focal point, the constructing rays of the image are
parallel and the image is at the infinity.Between the focal point and the center of the
lens, the image is virtual, upright, and enlarged comming from the left. There is absolutely
no image between the center of a converging lens and its right
focal point.
1. The simple magnifier
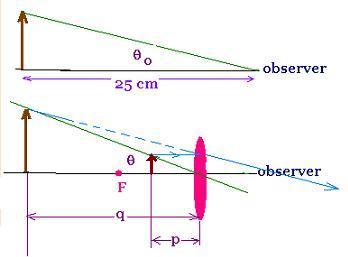 The more an object is near the observer, the more
the related angle formed by that object is large. For
the humain eye, the related length is about 25 cm.
We write tg θo = h/25 cm.
The length "h" is the height of the object.
The more an object is near the observer, the more
the related angle formed by that object is large. For
the humain eye, the related length is about 25 cm.
We write tg θo = h/25 cm.
The length "h" is the height of the object.
tg θ = h/p
The angular magnification is defined as
m = θ/θo = (h/p)/(h/25 cm) = 25cm/p
The angular magnification is maximum when the
angle θ is maximum, that is when the image formed
by the converging lens is at q = - 25 cm.
Now, We want an expression of the angular magnification "m".
1/p + 1/q = 1/f, so
1/p = 1/f - 1/q = (q - f)/qf, then:
p = qf/(q - f)
The angles θ and θo are small, so
θo = tg θo = h/25 cm, and
θ = tg θ = h/p
Therefore:
mmax = (h/p)/(h/25cm) = 25cm/P = 25cm(q - f)/qf = 25cm(-25 cm - f)/(-25 cm)f
with q = - 25 cm, we have:
mmax = 25 cm(25 cm - f)/25 cm f = 25 cm /f + 1
Exactly, when the object is near the focal point, (p = f) , the
image should be formed at infinity to minimize eyestrain.
we have:
m = (h/f)/(h/25 cm)= 25cm/f
This is the magnification of the simple magnifier.
2. Compound microscope
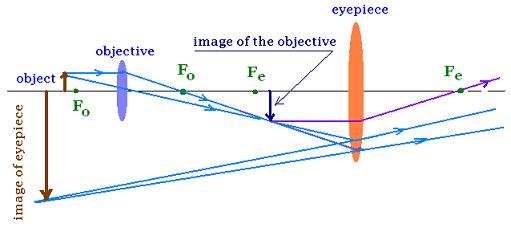 A compound microscope gives greater magnification than a
single lens. It contains two converging lenses: The
objective lens that has a short focal length
fo (< 1 cm) , and the eyepiece that
has a focal length, fe of a few cm.
A compound microscope gives greater magnification than a
single lens. It contains two converging lenses: The
objective lens that has a short focal length
fo (< 1 cm) , and the eyepiece that
has a focal length, fe of a few cm.
The linear magnification by the objective is
mo = - p/q
The angular magnification by the eyepiece of the
microscope is me = 25 cm / e
The total magnification mt of the
microscope is the product of the magnification by the
objective = mo = - q/p, and the
magnification by the eyepiece = me = 25cm/fe
mt = - (q/p)(25cm/fe)
Exactly, when the object is near the focal point, (p = fo),
and the first image is located at focal point of the eyepiece, the second
image virtual, inverted and magnified is formed at infinity.
If we set:
T = distance between the two focal points fe and fe.
It is called the tube length T. It is often set to 160 mm,
then:
mo = - q/p = - T/fo
therefore:
mt = - (T/f0)(25cm/fe) = - 25cm T/f0fe)
This is the often used magnification of the compound microscope.
|


