1. Image formed by a plane reflecting mirror
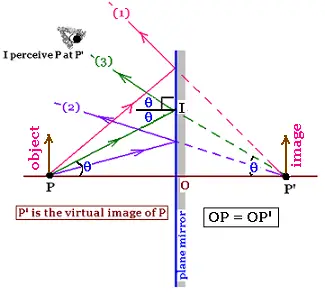
We perceive the image of an object "P" bacwards the mirror by the diverging rays
from the miror. The image is obtained by projeting rays that converge at the point
"P'". This image is virtual.
If we consider the ray (3), its reflection gives the angle θ at the point I.
Then the angle PP'I is equal to θ (corresponding angles). Thus, the triangle
PP'I is isocele. The line IO which is the height is then the bisectrix of this
triangle. Therefore PO = OP' and PP' is perpendicular to IO. The object and the image
are at the same distance from the mirror.
The image of the obect is erect (right side).
2. Mirror equation
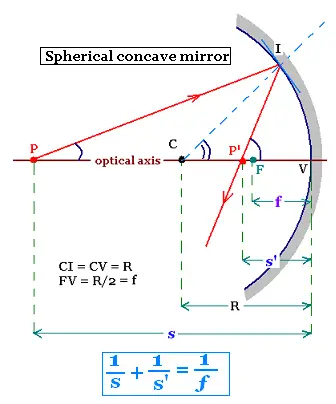
Curved mirrors are also used to form the image of an object. there are concave
spherical or convex spherical mirrors.
Let's consider a concave mirror of center C and radius of curvature R. The ray PI is
reflectef at the point I and then crosses the optical axis at the poit P'. CI = CV = R,
where V is the vertex of the spherical mirror. The line joininig P (object), C
center of the C, and the vertex is called optical axis. The light rays
that are not close to the optical axis blur (spherical aberration) the image of
an object conversely of the rays close to the optical axis called paraxial
rays. In Geometrical Optics, we always use only these rays.
The angles <PIC and <CIP' are equal because the ray IP' is
the reflected ray and the line IC is normal to the tangent fo the
cercle.
<PIP' = 2 <PIC
CPI + 2<CIP = IP'V (the exterior angle of a triangle is the sum of
the two opposite inteior angles)
Similarly,
CPI + CIP = ICV.
We have then:
<CPI + 2<CIP = <IP'V
<CPI + <CIP = <ICV
Eliminating the angle CIP, we find:
<CPI + <IP'V = 2 <ICV (1)
For paraxial rays, all these angles are small, they are the equal to their
radian measures, we can then write:
<CPI = IV/s
<CIP = IV/s'
<ICV = IV/R
The relationship (1) becomes:
IV/s + IV/s'= 2 IV/R
or
1/s + 1/s'= 2/R (2)
If the object is placed at a far distance (infinity) from
thr mirror, the length s becomes large, so 1/s becomes
small and neglected. Then s' = R/2 which means all the
reflected rays pass through the point F. The point F
is called the focal point of the mirror. It is
placed at the diatance VF from the vertex. This distance is
equal to ƒ = R/2, called focal length of the mirror.
Rewriting the relationship (2), it becomes:
1/s + 1/s'= 1/ƒ (3)
That is the mirror equation.
3. image formed by reflecting spherical mirrors: Mirror ray tracing
3.1. Magnification of an optical system
The magnification "m" of an optical system is the ratio of the image size
to the object size.
3.2. Concave mirror
There are three principal ray to trace to obtain the image of an object by graphical
construction:
(1). The incident parallel ray to the optical axis reflets to pass through the focal point.
(2).
The incident ray passing by the focal point reflets parallel to the optical axis.
(3).
The incident ray passing by the center of curvature of the mirror reflects back ton itself.
(0). The ray (0) is optional. It just shows the first law of reflection.
3.2.1. The object is far from the mirror
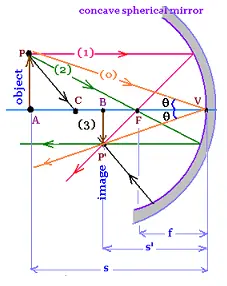
The object is far from the mirror:(FA >> FV). The rays from the object converge, then the
image is real. The image is inverted , then the magnification is negative:
BP'V and APV are similar, then:
m = BP'/AP = - s'/s
3.2.2. The object is between the vertex and the focal point of the mirror
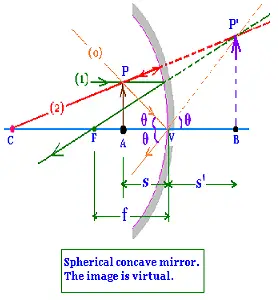
The object is located between the mirror and its focal point:(FA < FV). The ray from the obect diverge, then
he image is virtual. The image is right side up , then the magnification is positive.
BP'V and APV are similar, then:
m = BP'/AP = + s'/s
3.3. Convex mirror
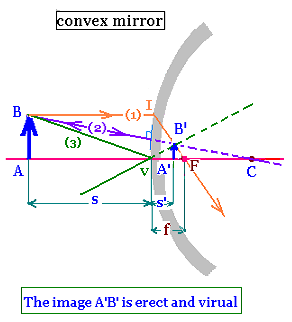
Two points are required to trace the image of the object. Ray (1) parallel to the
optica axis before reflection and diverges from the focal point F after
reflection; and ray (2) passing trough the centre of curvature of the sphere and
reflects back on itself. The image A'B' of the object AB is
pointed to the intersection of these rays.
For the convex mirror, we have also the mirror equation:
1/s + 1/s' = 1/f, and
m = s'/s
Indeed,
- The two triangles VAB and VA'B' are similar; then:
m = A'B'/AB = s'/s (1)
- The ywo triangles FVI and FA'B' are similar; then:
m = A'B'/VI = A'B'/AB = (f - s')/f (2)
The relationships (1) and (2) gives:
s'/s = (f - s')/f, so
fs' = sf - ss' or f (s - s') = ss'. Then
1/f = (s - s')/ss' = 1/s' - 1/s
f is negative, s' is also negative.
Therefore: 1/f = 1/s + 1/s'
4. Convention used for spherical mirrors
The position of an object and image is positive if they are real; negative
if they are virtual. The focal length is positive in concave and negative
in convex mirrors.
|


