1. Lens-makers' equation - thin lenses
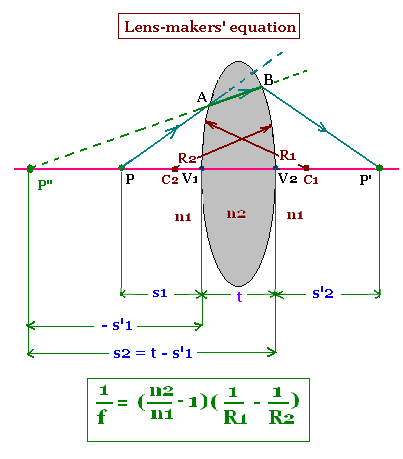
The image of the object "P" by the spherical convex interface of radius of curvature "R1 "
is the point P". This point is virtual because the
light ray is refracted from at "A" ("A" to "B"). The ray P"B (or AB) is refracted
by the spherical concave interface of radius of curvature "R2", and gives P' as the image
of the virtual point P".Finally, the image of the point P is P' by the two
interfaces forming a medium of index of refraction n2.
The position from the first vertex "V1",
of the object is V1P = s1, and the position of its image from this first vertex "V1" is
V1P" = - s'1 (it is negative).
Similarly, the position, from the second vertex "V2", of the point "P", is the one
of the point P", that is V2P" = s2 = t + (- s'1), and the position of its image from
this second vertex "V2" is V2P' = s'2. The parameter "t" stands for thikness of the
lens made up the block of index of refraction n2.
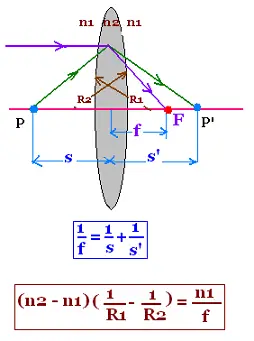
We have already found the following relationship, related to the refraction
of light ray by a convex spherical interface:
(n2 - n1)/R = n1/s + n2/s'. Rewriting this formula for the point
"P" requires two relationships: one (1) is related to the first interface
"R1", and the second (2) for the second interface "R2". We have:
(n2 - n1)/R1 = n1/s1 + n2/s'1 (1)
(n1 - n2)/R2 = n2/s2 + n1/s'2 (2)
Recombining (by adding) these two relationships, we obtain:
(n2 - n1)(1/R1 - 1/R2) = n1/s1 + n2/s'1 + n2/s2 + n1/s'2
We have also:
s2 = t + (- s'1) . The approximation for the thin lenses gives: t = 0; thus
s2 = -s'1. Therefore:
(n2 - n1)(1/R1 - 1/R2) = n1/s1 + n1/s'2
(3)
The focal length "ƒ" is defined as: If s1 tends to ∞ s'2 tends to ƒ,
then:
(n2 - n1)(1/R1 - 1/R2) = n1/ƒ
That is the Lens-makers' equation
According to this equation, the relationship (3) can be written as:
n1/ƒ = n1/s1 + n1/s'2. Or:
1/ƒ = 1/s + 1/s'
(3')
2. Converging and diverging thin lenses: rays tracing
2.1. converging lens:
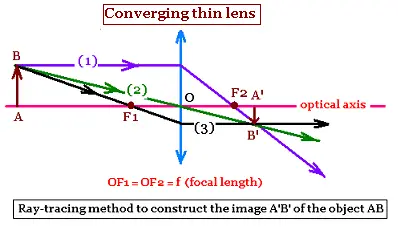
Two rays are essential to obtain the image of the object: Ray (1)
is parallel to the optic axis passes through the focal point F2; and
ray (2) passing undeviated through the center of the lens. The intersection
gives the point B'. A'B', prpendicular to the optic axis is the image
of the object AB. The image is real and inverted.
2. diverging lens:
|
|
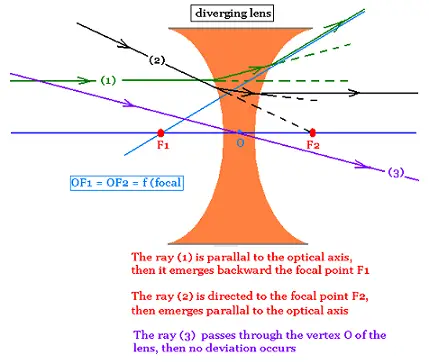
Two rays are essential to obtain the image of the object: Ray (1) is parallel to the optic axis and diverges from the focal point F1; and ray (2) passing undeviated through the center of the lens. The intersection gives the point B'. A'B', prpendicular to the optic axis is the image of the object AB. The image is virtual and right side up. 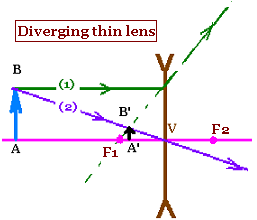
|